题目内容
8．
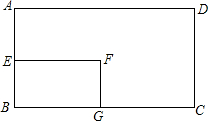如图，矩形ABCD的面积是72，AE=$\frac{1}{2}$DC，EF=$\frac{1}{2}$AD，那么矩形EBGF的面积是（ ）| A． | 24 | B． | 18 | C． | 12 | D． | 9 |
分析 先根据题意判断出矩形ABCD∽矩形EBGF，再由相似多边形的性质即可得出结论．
解答 解：∵AE=$\frac{1}{2}$DC，EF=$\frac{1}{2}$AD，
∴矩形ABCD∽矩形EBGF，相似比为2：1．
∵矩形ABCD的面积是72，
∴$\frac{{S}_{矩形ABCD}}{{S}_{矩形EBGF}}$=$\frac{72}{{S}_{矩形EBGF}}$=（$\frac{2}{1}$）2，解得S矩形EBGF=$\frac{72}{4}$=18．
故选B．
点评 本题考查的是相似多边形的性质，熟知相似多边形对应边的比叫做相似比，面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
相关题目
18．
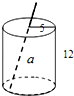如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）| A． | 5≤a≤12 | B． | 5≤a≤13 | C． | 12≤a≤13 | D． | 12≤a≤15 |
19．在△ABC中，∠C=90°，a=5，c=13，用计算器求∠A约等于（ ）
| A． | 14°38′ | B． | 65°22′ | C． | 67°23′ | D． | 22°37′ |
16．在Rt△ABC中，如果各边的长度都扩大2倍，那么锐角A的正弦值与余弦值（ ）
| A． | 都不变 | B． | 都扩大2倍 | C． | 都缩小$\frac{1}{2}$ | D． | 以上都不对 |
3．在△ABC中，∠C=90°，AC=3BC，则sinA=$\frac{\sqrt{10}}{10}$，cosA=$\frac{3\sqrt{10}}{10}$，tanA=$\frac{1}{3}$．
13．一列快车长306m，一列慢车长344m，两车相向而行，从相遇到离开需要13s，如果同向而行，快车从追及到超过慢车需要65s，求快车、慢车各自的速度．若设快车速度为x m/s，慢车速度为y m/s，那么，由题意列出的方程为（ ）
| A． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344\end{array}$ | B． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344+306\end{array}$ | ||
| C． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344-306\end{array}$ | D． | $\left\{\begin{array}{l}344y=306x\\ 65（x-y）=344+306\end{array}$ |
17．已知△ABC与△A′B′C′的相似比为1：2，△ABC的周长为30cm，并且△A′B′C′的三边比为4：5：6，则△A′B′C′的最长边为（ ）
| A． | 44cm | B． | 40cm | C． | 36cm | D． | 24cm |