题目内容
7.在△ABC中,∠C=90°,b=3,c=2$\sqrt{3}$,则∠A=30°,∠B=60°.分析 根据勾股定理求出a的值,然后根据三角函数的定义求出∠A和∠B的度数.
解答 解:在△ABC中,
∵∠C=90°,b=3,c=2$\sqrt{3}$,
∴a=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$,
则sinA=$\frac{a}{c}$=$\frac{\sqrt{3}}{2\sqrt{3}}$=$\frac{1}{2}$,
∠A=30°,
∴∠B=90°-30°=60°.
故答案为:30°,60°.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
17.下列判断中,正确的是( )
| A. | 0的绝对值是0 | B. | $\frac{22}{7}$是无理数 | C. | 4的平方根是2 | D. | 1的倒数是-1 |
18.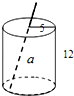 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )| A. | 5≤a≤12 | B. | 5≤a≤13 | C. | 12≤a≤13 | D. | 12≤a≤15 |
19.在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于( )
| A. | 14°38′ | B. | 65°22′ | C. | 67°23′ | D. | 22°37′ |
16.在Rt△ABC中,如果各边的长度都扩大2倍,那么锐角A的正弦值与余弦值( )
| A. | 都不变 | B. | 都扩大2倍 | C. | 都缩小$\frac{1}{2}$ | D. | 以上都不对 |
17.已知△ABC与△A′B′C′的相似比为1:2,△ABC的周长为30cm,并且△A′B′C′的三边比为4:5:6,则△A′B′C′的最长边为( )
| A. | 44cm | B. | 40cm | C. | 36cm | D. | 24cm |
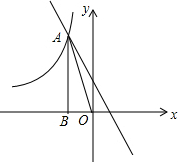 如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.
如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.


