题目内容
如图，△ABC为等边三角形，D为BC上一点，∠ADE=60°，DE交∠ACB外角平分线于E，求证：AD=DE．考点：全等三角形的判定与性质,等边三角形的判定与性质
专题：证明题
分析：求出∠ACE=∠DCE=60°，然后判断出点A、C、D、E四点共圆，再根据在同圆或等圆中，同弧所对的圆周角相等可得∠EAD=∠DCE=60°，然后判断出△ADE是等边三角形，再根据等边三角形的三边相等证明即可．
解答：证明：∵CE是等边△ABC的外角平分线，
∴∠ACE=∠DCE=60°，
∴点A、C、D、E四点共圆，
∴∠EAD=∠DCE=60°，
又∵∠ADE=60°，
∴△ADE是等边三角形，
∴AD=DE．
∴∠ACE=∠DCE=60°，
∴点A、C、D、E四点共圆，
∴∠EAD=∠DCE=60°，
又∵∠ADE=60°，
∴△ADE是等边三角形，
∴AD=DE．
点评：本题考查了等边三角形的判定与性质，利用四点共圆求解更简便．
练习册系列答案
相关题目
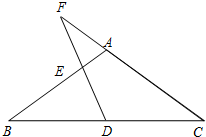如图，已知在△ABC中，AB=AC=10，BC=16，D是边BC的中点，E是射线BA上一动点，直线DE交射线CA于F点．
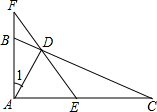如图，已知在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中点，ED交AB的延长线与F，
如图，抛物线y=x2-2x-3与x轴交于点A（-1，0），点B（3，0），与y轴交于点C，点D是该抛物线的顶点，连接AD，BD．
已知点B、C分别在∠MAN的两边上，BD⊥AM，CE⊥AN，垂足分别为D、E，BD、CE相交于点F，且BF=CF，试说明点F在∠A的平分线上．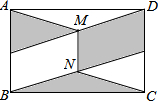
如图，在矩形ABCD中，点E、F分别是AB、CD的中点，连接DE和BF，分别取DE、BF的中点M、N，连接AM、CN、MN．若AB=3，BC=2