题目内容
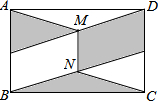 如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2
如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2| 5 |
考点:矩形的性质
专题:
分析:利用三角形中线的性质以及平行线的性质得出S△AEM=S△AMD,S△BNC=S△FNC,S四边形EBNM=S四边形DMNF,即可得出答案.
解答: 解:∵点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,
解:∵点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,
∴S△AEM=S△AMD,S△BNC=S△FNC,S四边形EBNM=S四边形DMNF,
∴图中阴影部分的面积=
×AB×BC=
×3×2
=3
.
故答案为:3
.
 解:∵点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,
解:∵点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,∴S△AEM=S△AMD,S△BNC=S△FNC,S四边形EBNM=S四边形DMNF,
∴图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
故答案为:3
| 5 |
点评:此题主要考查了矩形的性质以及三角形中线的性质,得出图中阴影部分的面积=
矩形ABCD是解题关键.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有个底角为60°,周长为40的等腰梯形,它的最大面积为( )
| A、20 | ||
B、50
| ||
| C、100 | ||
D、8
|
 图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )
图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )| A、72° | B、108° |
| C、144° | D、216° |
下列说法中,不正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、棱柱的侧面展开图是一个长方形 |
| C、若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的 |
| D、棱柱的上底面与下底面的形状与大小是完全一样的 |
若m、n、p是正整数,则(am•an)p等于( )
| A、am•anp |
| B、amp+np |
| C、amnp |
| D、amp•an |
 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE. 如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.
如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.