题目内容
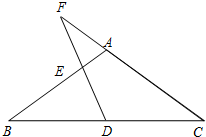 如图,已知在△ABC中,AB=AC=10,BC=16,D是边BC的中点,E是射线BA上一动点,直线DE交射线CA于F点.
如图,已知在△ABC中,AB=AC=10,BC=16,D是边BC的中点,E是射线BA上一动点,直线DE交射线CA于F点.(1)当DF=DC时,求AF的值;
(2)当点E位于线段AB上时(与B、A不重合),设BE=x,AF=y,求y关于x的函数解析式,并写出它的定义域;
(3)当△AEF为以FA腰的等腰三角形时,求x的值.
考点:相似三角形的判定与性质,等腰三角形的判定与性质
专题:常规题型
分析:(1)易证△ABC∽△DFC,根据
=
即可解题;
(2)易证△AFE∽△MDE,根据
=
可求出y关于x的函数解析式;
(3)分别求E位于线段AB上和BA的延长线上时x的值,即可解题.
| AC |
| DC |
| BC |
| CF |
(2)易证△AFE∽△MDE,根据
| AF |
| DM |
| AE |
| ME |
(3)分别求E位于线段AB上和BA的延长线上时x的值,即可解题.
解答:解:(1)∵AB=AC,
∴∠B=∠C,
∵DF=DC,
∴∠B=∠C,
∴∠B=∠F,
∴△ABC∽△DFC,
∴
=
,
∴
=
,
∴CF=12.8,
∴AF=2.8;
(2)取AB的中点M,联结DM.
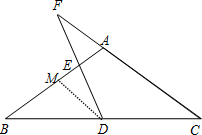
∵D是边BC的中点,
∴DM∥AC,DM=
AC=5,
∴△AFE∽△MDE,
∴
=
,
∴
=
,
∴y=
,
函数定义域为5<x<10;
(3)当点E位于线段AB上时,
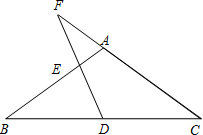
①若AF=AE 即
=10-x,
解得x=10 舍去,
②若AF=EFcos∠FAE=
,
5×
=
•(x-5)
x=
,
当点E位于线段BA延长线上时,此时y=
,
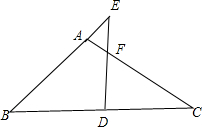
①若AF=AE 即
=x-10,
解得x=10舍去,
②若AF=EFcos∠FAE=
,
y=
(x-10)
解得x=
舍去.
综上所述,当△AEF为以FA腰的等腰三角形时,x=
.
∴∠B=∠C,
∵DF=DC,
∴∠B=∠C,
∴∠B=∠F,
∴△ABC∽△DFC,
∴
| AC |
| DC |
| BC |
| CF |
∴
| 10 |
| 8 |
| 16 |
| CF |
∴CF=12.8,
∴AF=2.8;
(2)取AB的中点M,联结DM.

∵D是边BC的中点,
∴DM∥AC,DM=
| 1 |
| 2 |
∴△AFE∽△MDE,
∴
| AF |
| DM |
| AE |
| ME |
∴
| y |
| 5 |
| 10-x |
| x-5 |
∴y=
| 5(10-x) |
| x-5 |
函数定义域为5<x<10;
(3)当点E位于线段AB上时,

①若AF=AE 即
| 5(10-x) |
| x-5 |
解得x=10 舍去,
②若AF=EFcos∠FAE=
| 7 |
| 25 |
5×
| 7 |
| 25 |
| 1 |
| 2 |
x=
| 39 |
| 5 |
当点E位于线段BA延长线上时,此时y=
| 5(x-10) |
| x-5 |

①若AF=AE 即
| 5(x-10) |
| x-5 |
解得x=10舍去,
②若AF=EFcos∠FAE=
| 7 |
| 25 |
| 7 |
| 25 |
| 1 |
| 2 |
解得x=
| 39 |
| 5 |
综上所述,当△AEF为以FA腰的等腰三角形时,x=
| 39 |
| 5 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
下列说法中正确的有( )
①±2都是8的立方根,②
=-2,③
的平方根是3,④-
=2.
①±2都是8的立方根,②
| (-2)2 |
| 81 |
| 3 | -8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )
图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )| A、72° | B、108° |
| C、144° | D、216° |
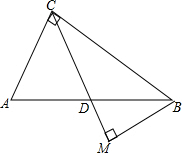 在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=
在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA= 如图,已知D,E分别是△ABC的AB,AC上的一点,DE∥BC,AB=7,AD=2,DE=4,求BC的长.
如图,已知D,E分别是△ABC的AB,AC上的一点,DE∥BC,AB=7,AD=2,DE=4,求BC的长. 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.