题目内容
 已知点B、C分别在∠MAN的两边上,BD⊥AM,CE⊥AN,垂足分别为D、E,BD、CE相交于点F,且BF=CF,试说明点F在∠A的平分线上.
已知点B、C分别在∠MAN的两边上,BD⊥AM,CE⊥AN,垂足分别为D、E,BD、CE相交于点F,且BF=CF,试说明点F在∠A的平分线上.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:易证△CDF≌△BFE,可得DF=EF,根据角平分线的性质即可判定F在∠A的平分线上.
解答:解:∵BD⊥AM,CE⊥AN
∴∠CDF=∠BEF,
在△CDF和△BFE中,
,
∴△CDF≌△BFE(AAS),
∴DF=EF,
∴F在∠A的平分线上.
∴∠CDF=∠BEF,
在△CDF和△BFE中,
|
∴△CDF≌△BFE(AAS),
∴DF=EF,
∴F在∠A的平分线上.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CDF≌△BFE是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
下列说法中正确的有( )
①±2都是8的立方根,②
=-2,③
的平方根是3,④-
=2.
①±2都是8的立方根,②
| (-2)2 |
| 81 |
| 3 | -8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
有个底角为60°,周长为40的等腰梯形,它的最大面积为( )
| A、20 | ||
B、50
| ||
| C、100 | ||
D、8
|
 图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )
图中的五角星绕旋转中心旋转后能与自身重合,则最小的旋转角度是( )| A、72° | B、108° |
| C、144° | D、216° |
 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.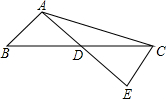 如图,在△ABC中,AB=8,AC=17,AD是边BC上的中线,E在AD的延长线上,AD=ED=
如图,在△ABC中,AB=8,AC=17,AD是边BC上的中线,E在AD的延长线上,AD=ED= 如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离.
如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离.
