题目内容
四个各不相等的整数a、b、c、d,它们的积abcd=49,那么a+b+c+d= .
考点:有理数的乘法,有理数的加法
专题:
分析:由于abcd=49,且a,b,c,d是整数,所以把49分解成四个不相等的整数的积,从而可确定a,b,c,d的值,进而求其和.
解答:解:∵49=1×(-1)×7×(-7),
∴a+b+c+d=1+(-1)+7+(-7)=0.
故答案为:0.
∴a+b+c+d=1+(-1)+7+(-7)=0.
故答案为:0.
点评:考查了有理数的乘法和加法,此题关键在于把49分解成四个不相等的整数的积,确定出四个数.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列说法中正确的有( )
①±2都是8的立方根,②
=-2,③
的平方根是3,④-
=2.
①±2都是8的立方根,②
| (-2)2 |
| 81 |
| 3 | -8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
有个底角为60°,周长为40的等腰梯形,它的最大面积为( )
| A、20 | ||
B、50
| ||
| C、100 | ||
D、8
|

 如图,正五边形ABCDE内接于⊙O,求∠ABD的度数.
如图,正五边形ABCDE内接于⊙O,求∠ABD的度数.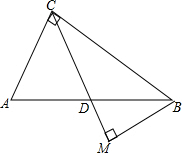 在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=
在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA= 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.