题目内容
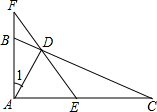 如图,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线与F,
如图,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线与F,(1)找出图中与∠1相等的角.
(2)求证:FD2=FB•FA.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)根据三角形内角和、内外角计算可以解题;
(2)求证△FBD∽△FDA,根据对应边比例相等,即可解题.
(2)求证△FBD∽△FDA,根据对应边比例相等,即可解题.
解答:解:(1)∵AD⊥BC,E是AC的中点,
∴AE=DE=CE,
∴∠CDE=∠C,
∵∠1+∠DAC=90°,∠C+∠DAC=90°,
∴∠1=∠C,
∵∠BDF=∠EDC,
∴∠1=∠C=∠CDE=∠BDF;
(2)∵∠F=∠F,∠1=∠BDF,
∴△FBD∽△FDA,
∴
=
,
∴DF2=AF•BF.
∴AE=DE=CE,
∴∠CDE=∠C,
∵∠1+∠DAC=90°,∠C+∠DAC=90°,
∴∠1=∠C,
∵∠BDF=∠EDC,
∴∠1=∠C=∠CDE=∠BDF;
(2)∵∠F=∠F,∠1=∠BDF,
∴△FBD∽△FDA,
∴
| AF |
| FD |
| FD |
| BF |
∴DF2=AF•BF.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
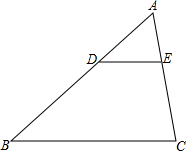 如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )
如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )| A、1:2 | B、1:4 |
| C、1:8 | D、1:9 |
 如图,正五边形ABCDE内接于⊙O,求∠ABD的度数.
如图,正五边形ABCDE内接于⊙O,求∠ABD的度数. 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.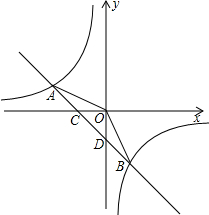 如图,反比例函数y=
如图,反比例函数y=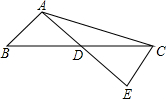 如图,在△ABC中,AB=8,AC=17,AD是边BC上的中线,E在AD的延长线上,AD=ED=
如图,在△ABC中,AB=8,AC=17,AD是边BC上的中线,E在AD的延长线上,AD=ED= 如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.
如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.