题目内容
 如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的
| 1 |
| 2 |
考点:抛物线与x轴的交点,二次函数的性质
专题:
分析:(1)利用抛物线与y轴交点求法得出C点坐标,再利用配方法求出其顶点坐标;
(2)利用D点坐标得出△ABD的面积;
(3)利用△ABD的面积得出△ABP的面积,进而求出P点纵坐标,进而求出其横坐标.
(2)利用D点坐标得出△ABD的面积;
(3)利用△ABD的面积得出△ABP的面积,进而求出P点纵坐标,进而求出其横坐标.
解答:解:(1)当x=0,则y=-3,
故C(0,-3),
y=x2-2x-3
=(x-1)2-4,
故D(1,-4);
(2)∵点A(-1,0),点B(3,0),
∴AB=4,
∴S△ABD=
×4×4=8;
(3)∵△ABP的面积是△ABD面积的
,
∴S△ABP=4,
∵AB=4,
∴P点纵坐标为2或-2,
当P点纵坐标为2,则2=x2-2x-3,
解得:x1=1+
,x2=1-
,
此时P点坐标为:(1+
,2)或(1-
,2),
当P点纵坐标为-2,则-2=x2-2x-3,
解得:x1=1+
,x2=1-
,
此时P点坐标为:(1+
,-2)或(1-
,-2),
综上所述:点P的坐标为:(1+
,2)、(1-
,2)、(1+
,-2)、(1-
,-2).
故C(0,-3),
y=x2-2x-3
=(x-1)2-4,
故D(1,-4);
(2)∵点A(-1,0),点B(3,0),
∴AB=4,
∴S△ABD=
| 1 |
| 2 |
(3)∵△ABP的面积是△ABD面积的
| 1 |
| 2 |
∴S△ABP=4,
∵AB=4,
∴P点纵坐标为2或-2,
当P点纵坐标为2,则2=x2-2x-3,
解得:x1=1+
| 6 |
| 6 |
此时P点坐标为:(1+
| 6 |
| 6 |
当P点纵坐标为-2,则-2=x2-2x-3,
解得:x1=1+
| 2 |
| 2 |
此时P点坐标为:(1+
| 2 |
| 2 |
综上所述:点P的坐标为:(1+
| 6 |
| 6 |
| 2 |
| 2 |
点评:此题主要考查了抛物线与x轴的交点以及三角形面积求法和二次函数图象上点的坐标性质等知识,注意分类讨论得出是解题关键.

练习册系列答案
相关题目
下列说法中,不正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、棱柱的侧面展开图是一个长方形 |
| C、若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的 |
| D、棱柱的上底面与下底面的形状与大小是完全一样的 |
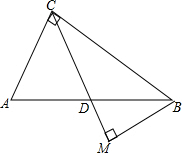 在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=
在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA= 如图,已知D,E分别是△ABC的AB,AC上的一点,DE∥BC,AB=7,AD=2,DE=4,求BC的长.
如图,已知D,E分别是△ABC的AB,AC上的一点,DE∥BC,AB=7,AD=2,DE=4,求BC的长. 如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE.
如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E,求证:AD=DE. 如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离.
如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离.