题目内容
18.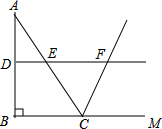 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 根据三角形中位线定理求出DE,得到DF∥BM,再证明EC=EF=$\frac{1}{2}$AC,由此即可解决问题.
解答 解:在RT△ABC中,∵∠ABC=90°,AB=8,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵DE是△ABC的中位线,
∴DF∥BM,DE=$\frac{1}{2}$BC=3,
∴∠EFC=∠FCM,
∵∠FCE=∠FCM,
∴∠EFC=∠ECF,
∴EC=EF=$\frac{1}{2}$AC=5,
∴DF=DE+EF=3+5=8.
故选B.
点评 本题考查三角形中位线定理、等腰三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用三角形中位线定理,掌握等腰三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | a+2a=2a2 | B. | (-2ab2)2=4a2b4 | C. | a6÷a3=a2 | D. | (a-3)2=a2-9 |
7.$\root{3}{8}$的算术平方根是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |

 如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.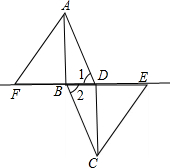 如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.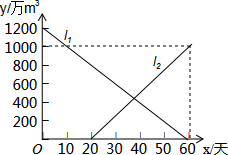 由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).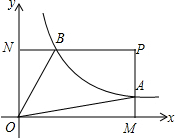 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.
如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.