题目内容
6.计算:(1)6÷(-3)+$\sqrt{4}$-8×2-2;
(2)解不等式组:$\left\{\begin{array}{l}{x-1<2}\\{\frac{x+1}{2}≥1}\end{array}\right.$.
分析 (1)根据实数的运算顺序,先计算除法、开方、乘方,再计算乘法,最后计算加减可得;
(2)分别求出每一个不等式的解集,根据口诀:大小小大中间找确定不等式组的解集.
解答 解:(1)原式=-2+2-8×$\frac{1}{4}$=-2;
(2)解不等式x-1<2,得:x<3,
解不等式$\frac{x+1}{2}$≥1,得:x≥1,
∴不等式组的解集为:1≤x<3.
点评 本题考查了实数的混合运算和一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
17. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 垂线段最短 | B. | 经过一点有无数条直线 | ||
| C. | 经过两点,有且仅有一条直线 | D. | 两点之间,线段最短 |
11.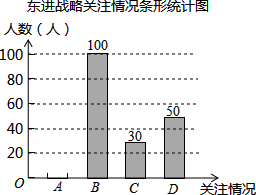 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
(1)根据上述统计图可得此次采访的人数为200人,m=20,n=0.15;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有1500人.
 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | M | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | N |
| D.不知道 | 50 | 0.25 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有1500人.
16.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知点C为反比例函数y=-$\frac{6}{x}$上一点,过点C向坐标轴引垂线,垂足分别为A,B,那么四边形AOBC的面积为( )
如图,已知点C为反比例函数y=-$\frac{6}{x}$上一点,过点C向坐标轴引垂线,垂足分别为A,B,那么四边形AOBC的面积为( ) 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)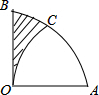 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.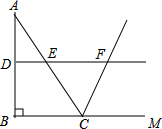 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )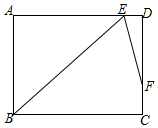 如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)
如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)