题目内容
10.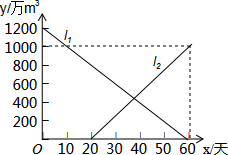 由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式,并求当x=20时的水库总蓄水量.
(2)求当0≤x≤60时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围),若总蓄水量不多于900万m3为严重干旱,直接写出发生严重干旱时x的范围.
分析 (1)根据两点的坐标求y1(万m3)与时间x(天)的函数关系式,并把x=20代入计算;
(2)分两种情况:①当0≤x≤20时,y=y1,②当20<x≤60时,y=y1+y2;并计算分段函数中y≤900时对应的x的取值.
解答 解:(1)设y1=kx+b,
把(0,1200)和(60,0)代入到y1=kx+b得:
$\left\{\begin{array}{l}{b=1200}\\{60k+b=0}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=-20}\\{b=1200}\end{array}\right.$,
∴y1=-20x+1200
当x=20时,y1=-20×20+1200=800,
(2)设y2=kx+b,
把(20,0)和(60,1000)代入到y2=kx+b中得:
$\left\{\begin{array}{l}{20k+b=0}\\{60k+b=1000}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=25}\\{b=-500}\end{array}\right.$,
∴y2=25x-500,
当0≤x≤20时,y=-20x+1200,
当20<x≤60时,y=y1+y2=-20x+1200+25x-500=5x+700,
y≤900,则5x+700≤900,
x≤40,
当y1=900时,900=-20x+1200,
x=15,
∴发生严重干旱时x的范围为:15≤x≤40.
点评 本题考查了一次函数的应用,熟练掌握利用待定系数法求一次函数的解析式:设直线解析式为y=kx+b,将直线上两点的坐标代入列二元一次方程组,求解;注意分段函数的实际意义,会观察图象.

练习册系列答案
相关题目
20.某校校园足球训练队队员的年龄有13、14、15、16四种年龄,统计结果如表:
根据表中信息可以判断该足球训练队队员年龄的众数为( )
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数(个) | 14 | 15 | 16 | 17 |
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
2.我国建造的长江三峡水电站,估计总装机容量达16780000千瓦,16780000用科学记数法表示为( )
| A. | 16.7×106 | B. | 1.68×107 | C. | 1.678×107 | D. | 1.678×108 |
20.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(1,a)、B(3,b),则a与b的关系正确的是( )
| A. | a=b | B. | a=-b | C. | a<b | D. | a>b |
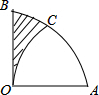 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.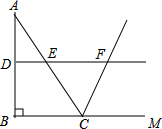 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( ) 昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.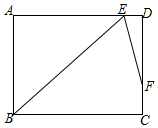 如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)
如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)