题目内容
8.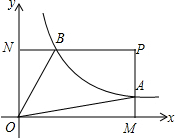 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.
如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.
分析 根据点P(6,3),可得点A的横坐标为6,点B的纵坐标为3,代入函数解析式分别求出点A的纵坐标和点B的横坐标,然后根据四边形OAPB的面积为12,列出方程求出k的值.
解答 解:∵点P(6,3),
∴点A的横坐标为6,点B的纵坐标为3,
代入反比例函数y=$\frac{k}{x}$得,
点A的纵坐标为$\frac{k}{6}$,点B的横坐标为$\frac{k}{3}$,
即AM=$\frac{k}{6}$,NB=$\frac{k}{3}$,
∵S四边形OAPB=12,
即S矩形OMPN-S△OAM-S△NBO=12,
6×3-$\frac{1}{2}$×6×$\frac{k}{6}$-$\frac{1}{2}$×3×$\frac{k}{3}$=12,
解得:k=6.
故答案为:6.
点评 本题考查了反比例函数系数k的几何意义,解答本题的关键是根据点A、B的纵横坐标,代入解析式表示出其坐标,然后根据面积公式求解.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
16.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(1,a)、B(3,b),则a与b的关系正确的是( )
| A. | a=b | B. | a=-b | C. | a<b | D. | a>b |
18.在平面直角坐标系中,点(1,5)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
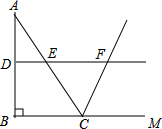 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )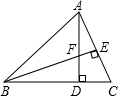 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.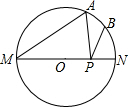 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为2$\sqrt{3}$.
如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为2$\sqrt{3}$.