题目内容
8.抛物线y=ax2+bx+4A(1,-1),B(5,-1),与y轴交于点C.(1)求抛物线的函数表达式;
(2)如图1,连接CB,若点P在直线BC上方的抛物线上,△BCP的面积为15,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为弧ACE上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.

分析 (1)将点A、B的坐标代入抛物线的解析式,得到关于a、b的方程,从而可求得a、b的值;
(2)设点P的坐标为P(m,m2-6m+4),根据S△CBP=15,由S△CBP=S梯形CEDP-S△CEB-S△PBD,得到关于m的方程求得m的值,从而可求得点P的坐标;
(3)首先证明△EAB∽△NMB,从而可得到NB=$\frac{3}{2}$,当MB为圆的直径时,NB有最大值.
解答 解:(1)将点A、B的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{a+b+4=-1}\\{25a+5b+4=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$.
∴抛物线得解析式为y=x2-6x+4;
(2)如图所示:
设点P的坐标为P(m,m2-6m+4)
∵S△CBP=15,即:S△CBP=S梯形CEDP-S△CEB-S△PBD,
∴$\frac{1}{2}$m(5+m2-6m+4+1)-$\frac{1}{2}$×5×5-$\frac{1}{2}$(m-5)(m2-6m+5)=15,
化简得:m2-5m-6=0,
解得:m=6,或m=-1,
∴点P的坐标为(6,4)或(-1,11),
(3)连接AB、EB,
∵AE是圆的直径,
∴∠ABE=90°,
∴∠ABE=∠MBN,
又∵∠EAB=∠EMB,
∴△EAB∽△NMB,
∵A(1,-1),B(5,-1),
∴点O1的横坐标为3,
将x=0代入抛物线的解析式得:y=4,
∴点C的坐标为(0,4),
设点O1的坐标为(3,m),
∵O1C=O1A,
∵OC=4,O1到OC的距离=3,
∴⊙O1的半径=$\sqrt{13}$,
∴$\sqrt{{3}^{2}+(m-4)^{2}}$=$\sqrt{13}$,
解得:m=2,
∴点O1的坐标为(3,2),
∴O1A=$\sqrt{{3}^{2}+(2-4)^{2}}$,
在Rt△ABE中,由勾股定理得:BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{(2\sqrt{13)^{2}-{4}^{2}}}$=6,
∴点E的坐标为(5,5),
∴AB=4,BE=6,
∵△EAB∽△NMB,
∴$\frac{AB}{EB}$=$\frac{MB}{NB}$,
∴$\frac{4}{6}$=$\frac{MB}{NB}$,
∴NB=$\frac{3}{2}$BM,
∴当MB为直径时,MB最大,此时NB最大,
∴MB=AE=2$\sqrt{13}$,
∴NB=$\frac{3}{2}$×2$\sqrt{13}$=3$\sqrt{13}$.
点评 本题主要考查了二次函数的综合应用,相似三角形的判定和性质,勾股定理,圆周角定理,利用两点间的距离公式求得圆的半径是解题的关键.

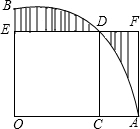 如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )
如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
| A. | (-ab3)2=a2b3 | B. | (x+3)2=x2+9 | C. | (-4)0=1 | D. | (-1)-3=1 |
| A. | m<$\frac{9}{2}$ | B. | m<$\frac{9}{2}$且m≠$\frac{3}{2}$ | C. | m>-$\frac{9}{4}$ | D. | m>-$\frac{9}{4}$且m≠-$\frac{3}{4}$ |
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数(个) | 14 | 15 | 16 | 17 |
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 垂线段最短 | B. | 经过一点有无数条直线 | ||
| C. | 经过两点,有且仅有一条直线 | D. | 两点之间,线段最短 |
 如图,已知点C为反比例函数y=-$\frac{6}{x}$上一点,过点C向坐标轴引垂线,垂足分别为A,B,那么四边形AOBC的面积为( )
如图,已知点C为反比例函数y=-$\frac{6}{x}$上一点,过点C向坐标轴引垂线,垂足分别为A,B,那么四边形AOBC的面积为( )
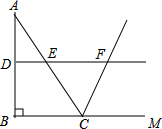 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )