题目内容
20.如图所示,
将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
分析 根据图象规律得出通项公式an=3n-3,根据数列{$\frac{9}{{a}_{n-1}{a}_{n}}$}的特点即可用列项法求其前n项和的公式,而$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$是前2016项的和,代入前n项和公式即可得答案.
解答 解:每个边上有n个点,把每个边上的点数相加得3n,这样角上的点数被重复计算了一次,
故第n个图形的点数为3n-3,即an=3n-3,
令Sn=$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{n-1}{a}_{n}}$=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)n}$=$\frac{n-1}{n}$,
∴$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=$\frac{2016}{2017}$,
故选:B.
点评 本题主要考查图形和数字的变化规律,根据图形得出点的变化规律和数字的变化规律是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,在?ABCD中,已知AB>BC.
如图,在?ABCD中,已知AB>BC.
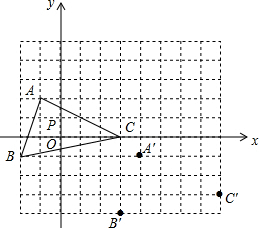 如图,△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0+5,y0-3),将△ABC作同样的平移得到△A′B′C′.
如图,△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0+5,y0-3),将△ABC作同样的平移得到△A′B′C′.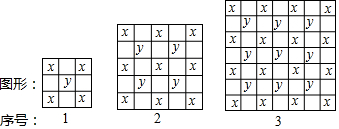
 如图,在△ABC中,AB=AC,∠B=30°,BC=12.
如图,在△ABC中,AB=AC,∠B=30°,BC=12.