题目内容
9. 如图,在△ABC中,AB=AC,∠B=30°,BC=12.
如图,在△ABC中,AB=AC,∠B=30°,BC=12.(1)用尺规作图的方法作AB的垂直平分线MN,分别交BC、AB于点M、N(保留作图痕迹,不要求写作法);
(2)求第(1)题中的CM的长.
分析 (1)根据尺规作图的方法,作AB的垂直平分线MN,分别交BC、AB于点M、N;
(2)根据线段垂直平分线的性质,得出∠BAM=∠B=30°,再根据等腰三角形的性质,即可得到∠CAM=90°,再根据含30度角的直角三角形的性质,得出MC=2AM=2BM,最后求得CM的长.
解答 解:(1)如图所示,MN即为所求;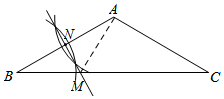
(2)如图,连结AM,
∵MN是AB的垂直平分线,
∴MB=MA
∴∠BAM=∠B=30°,
∴∠AMC=30°+30°=60°,
又∵AB=AC,
∴∠C=∠B=30°,
∴∠CAM=180°-60°-30°=90°,
∵在Rt△ACM中,∠C=30°,
∴MC=2AM=2BM,
又∵BC=12,
∴3BM=12,即BM=4,
∴MC=2BM=8.
点评 本题主要考查了基本作图,线段垂直平分线的性质,等腰三角形的性质以及含30度角的直角三角形的性质的综合应用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
20.如图所示,

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
17.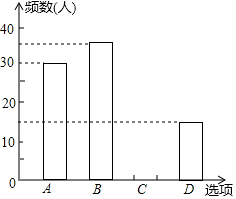 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=30,b=15,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
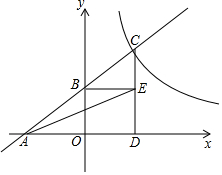 如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.
如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.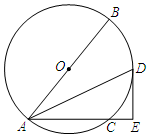 如图,⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作⊙O的切线交AC的延长线于点E.求DE的长.
如图,⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作⊙O的切线交AC的延长线于点E.求DE的长.
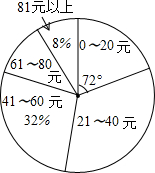 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题: