题目内容
12.观察下图: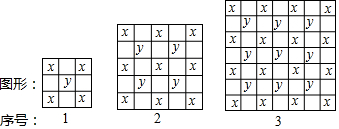
我们把正方形中所有x、y相加得到的多项式称为“正方形多项式”,如第1个图形中的“正方形多项式”为4x+y,第2个图形中的“正方形多项式”为9x+4y,遵循以上规律,解答下列问题:
(1)第4个图形中的“正方形多项式”为25x+16y,第n(n为正整数)个图形中的“正方形多项式”为(n+1)2x+n2y.
(2)如果第1个图形中的“正方形多项式”为5,第4个图形中的“正方形多项式”为2.
①求x和y的值;
②求“正方形多项式”的值Q的最大值(或最小值),并说明是第几个图形.
分析 (1)由前三个图形中正方形多项式知x的系数为序数加1的平方,y的系数为序数的平方,据此可得;
(2)①根据(1)中的结论,列出方程组解之可得x、y的值;
②由①中所求x、y的值代入可得Q=(n+1)2x+n2y=-n2+4n+2=-(n-2)2+6,据此即可知答案.
解答 解:(1)∵第1个图形中“正方形多项式”为:4x+y,
第2个图形中“正方形多项式”为:10x+4y,
第3个图形中“正方形多项式”为:16x+9y,
∴第4个图形中的“正方形多项式”为25x+16y,
第n(n为正整数)个图形中的“正方形多项式”为(n+1)2x+n2y,
故答案为:25x+16y,(n+1)2x+n2y;
(2)①依题意,得$\left\{\begin{array}{l}{4x+y=5}\\{25x+16y=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$;
②Q=(n+1)2x+n2y=-n2+4n+2=-(n-2)2+6,
当n=2时,Q最大值为6,
∴第2个图形中,“正方形多项式”的值最大,最大值为6.
点评 本题主要考查图形的变化规律和二次函数的性质,根据题意得出正方形多项式知x的系数为序数加1的平方,y的系数为序数的平方是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 6 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
20.如图所示,

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
7. 定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
 定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )| A. | 正五角形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
17.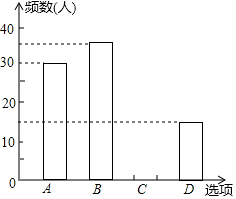 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=30,b=15,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
2.在等边三角形、平行四边形、矩形、菱形和圆中,既是轴对称图形又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
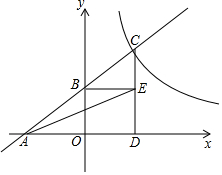 如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.
如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.