题目内容
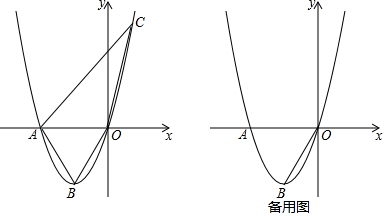
10.已知抛物线y=x2-2kx+k-1(1)求证:不论k取何值时,抛物线与x轴必有两个交点;
(2)设抛物线与x轴的两个交点分别为(x1,0)、(x2,0),求x12+x22的最小值.
分析 (1)根据方程的系数结合根的判别式,即可得出△=(2k-1)2+3>0,从而可得出不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根,即不论k取何值时,抛物线与x轴必有两个交点;
(2)由根与系数的关系可得出x1+x2=2k、x1•x2=k-1,将其代入x12+x22=(x1+x2)2-2x1•x2中,再利用配方法即可找出x12+x22的最小值.
解答 (1)证明:∵在关于x的一元二次方程x2-2kx+k-1=0中,△=(-2k)2-4(k-1)=(2k-1)2+3>0,
∴不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根,
∴不论k取何值时,抛物线与x轴必有两个交点.
(2)解:∵抛物线与x轴的两个交点分别为(x1,0)、(x2,0),
∴x1+x2=2k,x1•x2=k-1,
∴x12+x22=(x1+x2)2-2x1•x2=4k2-2k+2=4(k-$\frac{1}{4}$)2+$\frac{7}{4}$,
∴当k=$\frac{1}{4}$时,x12+x22取最小值,最小值为$\frac{7}{4}$.
点评 本题考查了抛物线与x轴的交点、二次函数的性质、二次函数的最值、根的判别式以及根与系数的关系,解题的关键是:(1)找出不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根;(2)利用配方法找出x12+x22的最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如图所示,

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
2.在等边三角形、平行四边形、矩形、菱形和圆中,既是轴对称图形又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
19.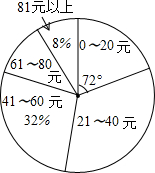 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
20.某种乐器的弦AB长为120cm,点A、B固定在乐器面板上,弦AB之间有一个支撑点C,且点C是AB的黄金分割点(AC>BC),则AC的长为( )
| A. | (120-30$\sqrt{5}$)cm | B. | (160-60$\sqrt{5}$)cm | C. | (60$\sqrt{5}$-120)cm | D. | (60$\sqrt{5}$-6)cm |