题目内容
8.如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD.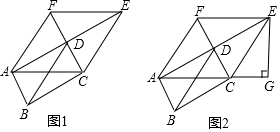
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG=$\frac{3}{5}$,则AD=2$\sqrt{5}$(直接填空)
分析 (1)先证明四边形ACEF是平行四边形,再由矩形的性质证出AE⊥CF,即可得出四边形ACEF是菱形;
(2)由菱形的性质得出AC=CE,AD=ED,与三角函数得出CG=$\frac{3}{5}$CE=$\frac{3}{5}$AC,得出CG=3,CE=AC=5,由勾股定理求出EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=4,在Rt△AEG中,由勾股定理求出AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=4$\sqrt{5}$,即可得出AD的长.
解答 (1)证明:∵DE=AD,DF=CD.
∴四边形ACEF是平行四边形,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴AE⊥CF,
∴四边形ACEF是菱形;
(2)解:∵四边形ACEF是菱形,
∴AC=CE,AD=ED,
∵EG⊥AC,cos∠ECG=$\frac{CG}{CE}$=$\frac{3}{5}$,
∴CG=$\frac{3}{5}$CE=$\frac{3}{5}$AC,
∵AG=AC+CG=8,
∴CG=3,CE=AC=5,
∴EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=4,
在Rt△AEG中,AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴AD=$\frac{1}{2}$AE=2$\sqrt{5}$;
故答案为:2$\sqrt{5}$.
点评 本题考查了矩形的性质、菱形的判定与性质、平行四边形的判定、勾股定理、三角函数定义等知识;熟练掌握矩形的性质,证明四边形ACEF是菱形是解决问题的关键.

练习册系列答案
相关题目
13. 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )| A. | $\frac{11π}{3}+2\sqrt{3}$ | B. | $3π+2\sqrt{3}$ | C. | $3π+\sqrt{3}$ | D. | $\frac{11π}{3}+\sqrt{3}$ |
20.如图所示,

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
17.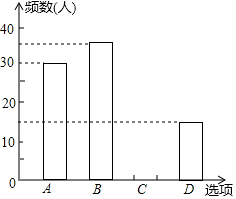 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=30,b=15,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?