题目内容
10.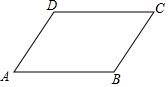 如图,在?ABCD中,已知AB>BC.
如图,在?ABCD中,已知AB>BC.(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;
(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.
分析 (1)作角平分线DE平分∠ADC,然后截取DF=AD;
(2)先利用证明四边形AEFD是平行四边形,然后利用AD=DF可判断□AEFD是菱形.
解答 解:(1)如图,AE和DF为所作;
(2)猜想:四边形AEFD是菱形.
证明:∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠CDE=∠DEA,
∵DE平分∠ADC,
∴∠CDE=∠ADE,
∴∠ADE=∠DEA,
∴AD=AE,
又∵AD=DF,
∴DF=AE且DF∥AE,
∴四边形AEFD是平行四边形,
∵AD=DF,
∴□AEFD是菱形.
点评 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了菱形的判定.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
9.下列各数中,比-2小的是( )
| A. | -1 | B. | -3 | C. | 0 | D. | $\frac{π}{2}$ |
10.-$\frac{1}{2017}$的相反数是( )
| A. | $\frac{1}{2017}$ | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | -2017 |
2. 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 6 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
20.如图所示,

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )

将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an ,则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |