题目内容
15．
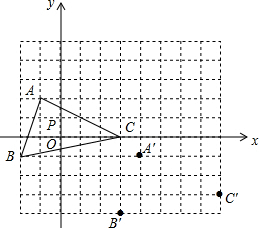如图，△ABC中任意一点P（x0，y0）经平移后对应点为P′（x0+5，y0-3），将△ABC作同样的平移得到△A′B′C′．（1）在图中画出△A′B′C′，并写出A′，B′，C′的坐标．
（2）求出△A′B′C′的面积．
分析 （1）根据图形平移的性质画出△A′B′C′，并写出各点坐标即可；
（2）利用矩形的面积减去三个顶点上三角形的面积即可．
解答 
解：（1）如图，△A′B′C′即为所求，A′（4，-1），B′（3，-4），C′（8，-3）；
（2）S△A′B′C′=3×5-$\frac{1}{2}$×1×5-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3
=15-$\frac{5}{2}$-4-$\frac{3}{2}$
=7．
点评 本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
相关题目
10．
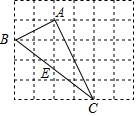如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，若点E是BC的中点，则sin∠CAE的值为（ ）
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，若点E是BC的中点，则sin∠CAE的值为（ ）| A． | 2 | B． | $\frac{1}{2}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
20．如图所示，
将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为an ，则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=（ ）
将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为an ，则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+…+$\frac{9}{{a}_{2017}{a}_{2018}}$=（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{2016}{2017}$ | C． | $\frac{2017}{2018}$ | D． | $\frac{2018}{2017}$ |
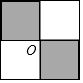定义：用形状、大小完全相同的一种或几种平面图进行拼接，彼此之间不留空隙，不重叠地铺成一片，称为平面图形的镶嵌，如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案．判断：若只选用一种大小相同的正多边形，在下列四个选项中，能进行平面镶嵌的是（ ）
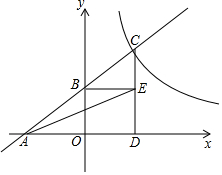如图，直线AB与x轴交于点A，与y轴交于点B，与双曲线y=$\frac{k}{x}$（k＞0）交于点C，过点C作CD⊥x轴于点D，过点B作BE⊥CD于点E，tan∠BCE=$\frac{3}{2}$，点E的坐标为（2，$\frac{3}{2}$），连接AE．