题目内容
18.已知关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0有两个实数根.(1)求k的取值范围;
(2)若方程的两实数根分别为x1,x2,且x12+x22=6x1x2-15,求k的值.
分析 (1)根据方程的系数结合根的判别式即可得出△=2k-3≥0,解之即可得出结论;
(2)由根与系数的关系可得,x1+x2=k+1、x1•x2=$\frac{1}{4}$k2+1,结合x12+x22=6x1x2-15即可得出关于k的一元二次方程,解之即可得出k值,再由(1)的结论即可确定k值.
解答 解:(1)∵关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0有两个实数根,
∴△=[-(k+1)]2-4($\frac{1}{4}$k2+1)=2k-3≥0,
解得:k≥$\frac{3}{2}$.
(2)∵方程的两实数根分别为x1,x2,
∴x1+x2=k+1,x1•x2=$\frac{1}{4}$k2+1.
∵x12+x22=6x1x2-15,
∴$({x}_{1}+{x}_{2})^{2}$-8x1x2+15=0,
∴k2-2k-8=0,
解得:k1=4,k2=-2.
又∵k≥$\frac{3}{2}$,
∴k=4.
点评 本题考查了根与系数的关系、根的判别式以及解一元二次方程,解题的关键是:(1)由方程解得个数结合根的判别式找出△=2k-3≥0;(2)利用根与系数的关系找出k2-2k-8=0.

练习册系列答案
相关题目
13.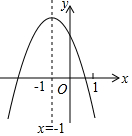 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②3a+c<0;③(a+c)2>b2;④x(ax+b)≤a-b.
其中正确结论的个数是( )
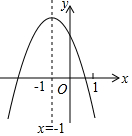 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②3a+c<0;③(a+c)2>b2;④x(ax+b)≤a-b.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
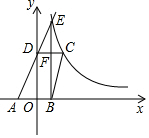 如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
 如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )
如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )