题目内容
10.写字时一项主要基本功,也是素质教育的重要部分,为了了解我校学生的书写情况,随机对部分学生进行测试,测试结果分为四个等级:优秀、良好、合格、不合格;根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息,回答以下问题:
(1)扇形统计图中,“合格”的百分比为40%;
(2)本次抽测不合格等级学生有16人;
(3)随机抽取了5名等级为“优秀”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,求刚好抽到同性别学生的概率;
(4)若该校共有2000名学生,估计该校书写“不合格”等级学生约有多少人?
分析 (1)用1分别减去其它各等级的百分比即可得到“合格”的百分比;
(2)先利用优秀等级的人数和它所占的百分比得到样本容量,再计算出本次抽测不合格等级学生;
(3)画树状图展示所有20种等可能的结果数,再找出抽到同性别学生的结果数,然后根据概率公式求解;
(4)利用样本估计整体,用2000乘以样本中不合格”等级学生的百分比即可.
解答 解:(1)扇形统计图中,“合格”的百分比=1-32%-16%-12%=40%;
(2)8÷16%=50,则本次抽测不合格等级学生数=50×32%=16(人);
故答案为40%,16;
(3)画树状图为: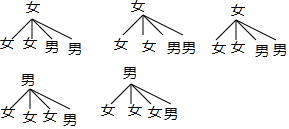
共有20种等可能的结果数,其中抽到同性别学生的结果数为8,
所以刚好抽到同性别学生的概率=$\frac{8}{20}$=$\frac{2}{5}$;
(4)2000×32%=640,
所以估计该校书写“不合格”等级学生约有640人.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
1.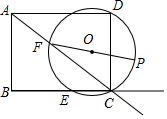 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )
 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{4}$π | C. | $\frac{15}{2}$ | D. | $\frac{15}{2}$π |
20.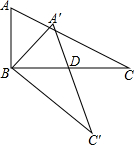 如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )
如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )
 如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )
如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )| A. | $\frac{4\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
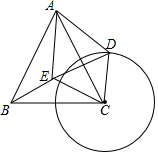 如图,正△ABC的边长为2,⊙C的半径为1,点D在⊙C上,以AD为边作正△ADE,连接CD、CE、BE.
如图,正△ABC的边长为2,⊙C的半径为1,点D在⊙C上,以AD为边作正△ADE,连接CD、CE、BE. 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.