题目内容
6.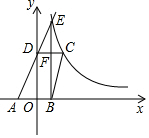 如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.(1)若EB=$\frac{4}{3}$OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
分析 (1)根据点C坐标求出反比例函数的解析式,再求出点E的纵坐标,即可解决问题.
(2)设E(m,$\frac{6}{m}$),则B(m,0),由四边形ABCD是平行四边形,推出CD=AB=2,由DF∥AB,推出$\frac{DF}{AB}$=$\frac{EF}{EB}$,推出$\frac{m}{2}$=$\frac{\frac{6}{m}-3}{\frac{6}{m}}$,解得m=1,可得E(1,6),设直线AD的解析式为y=kx+b,利用待定系数法即可解决问题.
解答 解:(1)∵C(2,3),
把C(2,3)代入y=$\frac{k}{x}$中,k=6,
∴y=$\frac{6}{x}$,
∵CD⊥y轴,
∴OD=3,
∵BE=$\frac{4}{3}$OD,
∴BE=4,
∴y=4时,4=$\frac{6}{x}$,
∴x=$\frac{3}{2}$,
∴点E坐标($\frac{3}{2}$,4);
(2)设E(m,$\frac{6}{m}$),则B(m,0),
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵DF∥AB,
∴$\frac{DF}{AB}$=$\frac{EF}{EB}$,
∴$\frac{m}{2}$=$\frac{\frac{6}{m}-3}{\frac{6}{m}}$,
解得m=1,
∴E(1,6),
设直线AD的解析式为y=kx+b,则有$\left\{\begin{array}{l}{k+b=6}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AD的解析式为y=3x+3.
点评 本题考查反比例函数的解析式、一次函数的应用、平行四边形的性质、平行线分线段成比例定理等知识,解题的关键是熟练掌握待定系数法解决问题,学会用构建方程的思想思考问题,属于中考压轴题.

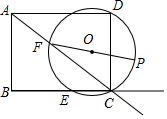 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点B出发,沿射线BC移动,过D、C、E三点作⊙O,点F为⊙O与射线AC的公共点,过F作⊙O的直径FP.当圆O与射线AC相切时,点E停止移动,在点E移动的过程中,点P移动路径的长( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{4}$π | C. | $\frac{15}{2}$ | D. | $\frac{15}{2}$π |
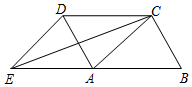 如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )
如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )| A. | AB=AD | B. | AB=ED | C. | CD=AE | D. | EC=AD |
 如图,在△ABC中,∠ACB=58°,若P为△ABC内一点,且∠1=∠2,则∠BPC=122°.
如图,在△ABC中,∠ACB=58°,若P为△ABC内一点,且∠1=∠2,则∠BPC=122°. 如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.
如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.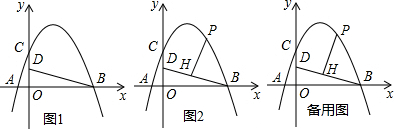
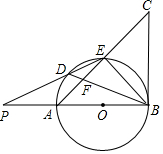 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.