题目内容
某宾馆有客房90间,当每间客房的定价为每天140元时,客房会全部住满,当每间客房每天的定价每涨10元时,就会有5间客房空闲.游客居住客房,宾馆需对每间客房每天支出60元的各种费用.空闲房间不支付各种费用,设每间客房每天的定价涨x个10元.(x为非负整数)
(1)设某天的利润为8000元,求相应的x;
(2)判断8000元的利润是否为每天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?
(1)设某天的利润为8000元,求相应的x;
(2)判断8000元的利润是否为每天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?
考点:二次函数的应用,一元二次方程的应用
专题:销售问题
分析:(1)设每间客房涨价10x元,根据题意列出方程,在涨价后的房间数乘以房间价格等于获利的8000元,解出x即可;
(2)把(1)的函数关系式用配方法化简可得y=-50(x-5)2+8450,利用二次函数的性质进行解答.
(2)把(1)的函数关系式用配方法化简可得y=-50(x-5)2+8450,利用二次函数的性质进行解答.
解答:解:(1)设每间客房涨价10x元,根据题意,
得(140+10x-60)(90-5x)=8000.(4分)
x2-10x+16=0.
x1=2,x2=8.
因为尽可能节约资源,所以x=2舍去.
答:设某天的利润为8000元,相应的x的值是8;
(2)8000元的利润不是为该天的最大利润.理由如下:
设每天的利润为w,则由(1)知,
w=(140+10x-60)(90-5x)=-50(x-5)2+8450
∴当x=5时,w最大=8450.
则每间客房的定价为:140+10×5=190(元)
答:即每间客房定价为190元时,宾馆当天的最大利润为8450元.
得(140+10x-60)(90-5x)=8000.(4分)
x2-10x+16=0.
x1=2,x2=8.
因为尽可能节约资源,所以x=2舍去.
答:设某天的利润为8000元,相应的x的值是8;
(2)8000元的利润不是为该天的最大利润.理由如下:
设每天的利润为w,则由(1)知,
w=(140+10x-60)(90-5x)=-50(x-5)2+8450
∴当x=5时,w最大=8450.
则每间客房的定价为:140+10×5=190(元)
答:即每间客房定价为190元时,宾馆当天的最大利润为8450元.
点评:本题考查了二次函数的应用,要求同学们仔细审题,将实际问题转化为数学模型,注意配方法求二次函数最值的应用.

练习册系列答案
相关题目
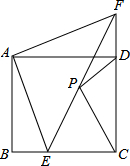 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.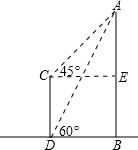 某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(
某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(
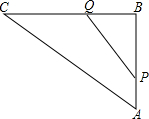 如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.
如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动. 如图,点A(a,1)、B(-1,b)都在双曲线y=-
如图,点A(a,1)、B(-1,b)都在双曲线y=-