题目内容
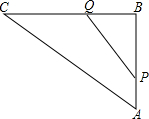 如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.
如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.(1)20s后,点P与点Q之间相距
(2)在(1)的条件下,若P、Q两点同时相向而行,
(3)多少秒后,AP=CQ?
考点:勾股定理,一元一次方程的应用
专题:动点型
分析:(1)在直角△BPQ中,根据勾股定理来求PQ的长度;
(2)由(1)中的PQ=50得到:50=(1+1.5)t;
(3)由路程=时间×速度列出等式.
(2)由(1)中的PQ=50得到:50=(1+1.5)t;
(3)由路程=时间×速度列出等式.
解答:解: 如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,
如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,
∴AB=
=60cm.
(1)在直角△BPQ中,由勾股定理得到:PQ=
=
=50(cm),即PQ=50cm;
(2)由(1)知,PQ=50cm,则P、Q两点同时相向而行时,两点相遇的时间为:
=20(秒);
(3)设t秒后,AP=CQ.则
t=80-1.5t,
解得 t=32.
答:32秒后,AP=CQ.
故答案是:(1)50 (2)20 (3)32.
 如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,
如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,∴AB=
| AC2-BC2 |
(1)在直角△BPQ中,由勾股定理得到:PQ=
| BQ2+BP2 |
| (1.5×20)2+(60-20)2 |
(2)由(1)知,PQ=50cm,则P、Q两点同时相向而行时,两点相遇的时间为:
| 50 |
| 1+1.5 |
(3)设t秒后,AP=CQ.则
t=80-1.5t,
解得 t=32.
答:32秒后,AP=CQ.
故答案是:(1)50 (2)20 (3)32.
点评:本题考查了勾股定理和一元一次方程的定义.解题时,需要熟悉路程=时间×速度,以及变形后的公式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
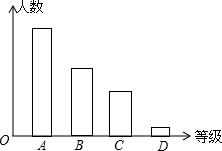 吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: 如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.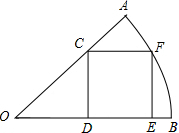 如图,在半径为
如图,在半径为