题目内容
 如图,点A(a,1)、B(-1,b)都在双曲线y=-
如图,点A(a,1)、B(-1,b)都在双曲线y=-| 2 |
| x |
考点:轴对称-最短路线问题,反比例函数图象上点的坐标特征
专题:
分析:先把A点坐标和B点坐标代入反比例函数进行中可确定点A的坐标为(-2,1)、B点坐标为(-1,2),再作A点关于x轴的对称点C,B点关于y轴的对称点D,根据对称的性质得到C点坐标为(-2,-1),D点坐标为(1,2),CD分别交x轴、y轴于P点、Q点,根据两点之间线段最短得此时四边形PABQ的周长最小,然后利用待定系数法确定PQ的解析式.
解答:解:分别把点A(a,1)、B(-1,b)代入双曲线y=-
得a=-2,b=2,则点A的坐标为(-2,1)、B点坐标为(-1,2),
作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(-2,-1),D点坐标为(1,2),
连结CD分别交x轴、y轴于P点、Q点,此时四边形PABQ的周长最小,
设直线CD的解析式为y=kx+b,
把C(-2,-1),D(1,2)分别代入
,
解得
,
所以直线CD的解析式为y=x+1.
故答案为:y=x+1.
| 2 |
| x |

作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(-2,-1),D点坐标为(1,2),
连结CD分别交x轴、y轴于P点、Q点,此时四边形PABQ的周长最小,
设直线CD的解析式为y=kx+b,
把C(-2,-1),D(1,2)分别代入
|
解得
|
所以直线CD的解析式为y=x+1.
故答案为:y=x+1.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、待定系数法求一次函数的解析式;熟练运用两点之间线段最短解决有关几何图形周长最短的问题.

练习册系列答案
相关题目
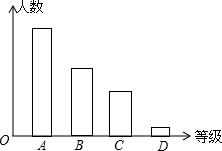 吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: 如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.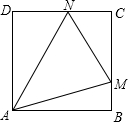 如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为
如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为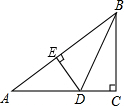 如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是
如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是