题目内容
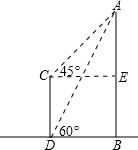 某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(
某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△ADB、△ACE,应利用其公共边DB=200m,构造等量关系式,进而可求出答案.
解答:解:设楼高CD=xm,
∵CE=BD=200,∠ACE=45°,
∴AE=CE•tan45°=200(m).
∴AB=100+x.
在Rt△ADB中,
∵∠ADB=60°,∠ABD=90°,
∴
=tan60°,
∴AB=
BD,
即x+200=200
,
解得:x=200
-200≈146.4(m),
则塔高为:146.4+200=346.4(m).
答:楼高约146.4,塔高约346.4m.
∵CE=BD=200,∠ACE=45°,
∴AE=CE•tan45°=200(m).
∴AB=100+x.
在Rt△ADB中,
∵∠ADB=60°,∠ABD=90°,
∴
| AB |
| BD |
∴AB=
| 3 |
即x+200=200
| 3 |
解得:x=200
| 3 |
则塔高为:146.4+200=346.4(m).
答:楼高约146.4,塔高约346.4m.
点评:本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)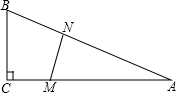 如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
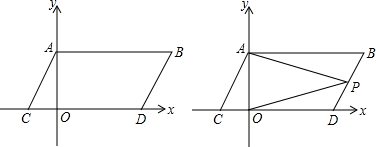
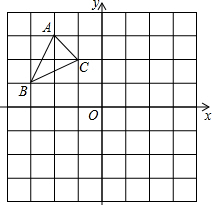 △ABC在如图的平面直角坐标系中,
△ABC在如图的平面直角坐标系中,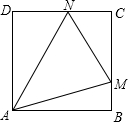 如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为
如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为