题目内容
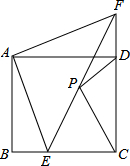 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:AE=AF;
(2)若∠AEB=75°,求∠CPD的度数.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得∠B=∠ADC=∠ADF=90°,AB=AD,结合BE=DF,即可证明△ABE≌△ADF,于是可得AE=AF;
(2)连结AP,首先根据△ABE≌△ADF得∠BAE=∠DAF,结合角角之间的关系得到∠CEF=60°,由P为EF中点,∠EAF=90°,AP=
EF,得到AO=CP,进一步证明△APD≌△CPD,再根据三角形全等的性质得∠ADP=∠CDP,进而求出∠CPD的度数.
(2)连结AP,首先根据△ABE≌△ADF得∠BAE=∠DAF,结合角角之间的关系得到∠CEF=60°,由P为EF中点,∠EAF=90°,AP=
| 1 |
| 2 |
解答:解:(1)∵四边形ABCD为正方形,
∴∠B=∠ADC=∠ADF=90°,AB=AD,
又∵BE=DF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)连结AP,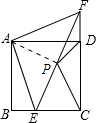
∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
又∵AE=AF,
∴∠AEF=45°,
∵∠AEB=75°,
∴∠CEF=180°-45°-75°=60°,
∵∠ECF=90°,P为EF中点,
∴CP=PF=
EF,∠EFC=∠PCF=30°,
∵P为EF中点,∠EAF=90°,AP=
EF,
∴AP=CP,
又∵AD=CD,PD=PD,
在△APD和△CPD中,
,
∴△APD≌△CPD(SSS),
∴∠ADP=∠CDP,
∵∠ADC=90°,
∴∠CDP=45°,
∴∠CPD=180°-∠PCD-∠CDP=105°.
∴∠B=∠ADC=∠ADF=90°,AB=AD,
又∵BE=DF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)连结AP,

∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
又∵AE=AF,
∴∠AEF=45°,
∵∠AEB=75°,
∴∠CEF=180°-45°-75°=60°,
∵∠ECF=90°,P为EF中点,
∴CP=PF=
| 1 |
| 2 |
∵P为EF中点,∠EAF=90°,AP=
| 1 |
| 2 |
∴AP=CP,
又∵AD=CD,PD=PD,
在△APD和△CPD中,
|
∴△APD≌△CPD(SSS),
∴∠ADP=∠CDP,
∵∠ADC=90°,
∴∠CDP=45°,
∴∠CPD=180°-∠PCD-∠CDP=105°.
点评:本题主要考查正方形的性质,解答本题的关键是熟练掌握正方形的性质以及全等三角形的证明.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)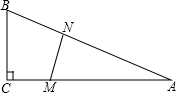 如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.