题目内容
9.解方程:$\frac{2x}{x+1}$=$\frac{4x}{2x+2}$+1.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:方程两边都乘以2(x+1)得:4x=4x+2x+2,
解得:x=-1,
经检验x=-1是增根,分式方程无解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
1.下列各式正确的是( )
| A. | ${x^6}•{x^{-2}}={x^{-12}}=\frac{1}{{{x^{12}}}}$ | B. | ${x^6}÷{x^{-2}}={x^{-3}}=\frac{1}{x^3}$ | ||
| C. | ${(x{y^{-2}})^3}={x^3}{y^{-2}}=\frac{x^3}{y^2}$ | D. | ${({\frac{y^3}{x^2}})^{-1}}=\frac{x^2}{y^3}$ |
18.在下列长度的各组线段中,能组成直角三角形的是( )
| A. | 5,6,7 | B. | $\sqrt{2}$,$\sqrt{5}$,$\sqrt{7}$ | C. | 1,4,9 | D. | 5,11,12 |
19.在一个不透明的袋子中装有仅有颜色不同的10个球,其中红球4个,白球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“再从袋子中随机摸出一个球是白球”记为事件A,请完成下表:
(2)先从袋子中取出m个红球,再放入m个相同的白球并摇匀,随机摸出一个球是白球的概率等于$\frac{4}{5}$,求m的值.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“再从袋子中随机摸出一个球是白球”记为事件A,请完成下表:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2或3 |
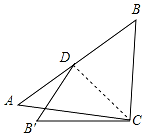 如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′=6°.
如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′=6°.