题目内容
7．
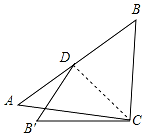如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=48°，则∠ACB′=6°．
分析 根据三角形内角和定理求出∠A的度数，根据直角三角形的性质分别求出∠BCD、∠DCA的度数，根据翻折变换的性质求出∠B′CD的度数，计算即可．
解答 解：∵∠ACB=90°，∠B=48°，
∴∠A=42°，
∵∠ACB=90°，CD是斜边上的中线，
∴CD=BD，CD=AD，
∴∠BCD=∠B=48°，∠DCA=∠A=42°，
由翻折变换的性质可知，∠B′CD=∠BCD=48°，
∴∠ACB′=∠B′CD-∠DCA=6°，
故答案为：6°．
点评 本题考查的是直角三角形的性质、翻折变换的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
18．
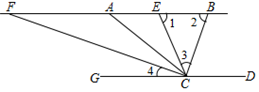如图，CD∥AB，BC平分∠ACD，CF平分∠ACG，
∠BAC=40°，∠1=∠2，则下列结论：
①CB⊥CF；②∠1=70°；③∠ACE=2∠4；④∠3=2∠4，
其中正确的是（ ）
如图，CD∥AB，BC平分∠ACD，CF平分∠ACG，∠BAC=40°，∠1=∠2，则下列结论：
①CB⊥CF；②∠1=70°；③∠ACE=2∠4；④∠3=2∠4，
其中正确的是（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③④ | D． | ①②③④ |
2．能判断一个四边形是平行四边形的为（ ）
| A． | 一组对边平行，另一组对边相等 | B． | 一组对边平行，一组对角相等 | ||
| C． | 一组对边平行，一组对角互补 | D． | 一组对边平 行，两条对角线相等 |
如图，AB是⊙O的直径，点C在⊙O上，OD∥AC，交BC于D．若BD=1，则BC的长为2．