题目内容
20.这是课本第二章第5节的一道例题:例1已知如图1,在△ABC中,AB=AC,点D在BC上,且AD=BD.
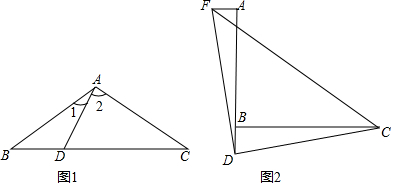
求证:∠ADB=∠BAC.
课本旁边有这样的“思考与表述”:
怎么想:
要证∠ADB=∠BAC,
由于∠BAC=∠1+∠2,
∠ADB=∠C+∠2,
只要证∠1=∠C.
只要找与∠1相等且与∠C也相等的角.
猜想∠1=∠B,∠C=∠B.而己知AD=BD,AB=AC.
这种思考方法称为分析法,就是从结论出发,要证什么,需证什么,一步步倒推上去,
直到和已知条件吻合.
试仿照上面的“怎么想”用分析法写出下面这道题的分析过程.
如图2,已知∠ABC=90°,D是直线AB上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF.求证:△CDF是等腰直角三角形.
解:怎么想:
分析 首先证明△ADF≌△BCD得到DF=CD,∠ADF=∠BCD,再利用∠BCD+∠CDB=90°得到∠CDF=90°,则可判断△CDF为等腰直角三角形;
解答 证明:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中
$\left\{\begin{array}{l}{AF=DB}\\{∠DAF=∠CBD}\\{AB=BC}\end{array}\right.$,
∴△ADF≌△BCD,
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴△CDF为等腰直角三角形.
点评 本题考查了全等三角形的判定与性质全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
18.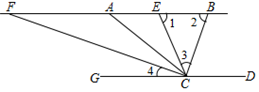 如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,
如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,
∠BAC=40°,∠1=∠2,则下列结论:
①CB⊥CF;②∠1=70°;③∠ACE=2∠4;④∠3=2∠4,
其中正确的是( )
 如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,
如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:
①CB⊥CF;②∠1=70°;③∠ACE=2∠4;④∠3=2∠4,
其中正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
12.在实数3.14,0,$\frac{22}{7}$,$\sqrt{12}$,π,1.6,$\root{3}{-125}$,0.121221222122221…(相邻两个1之间的2一次增加1)中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.扬州1月某日的最高气温是8°C,最低气温是1°C,这天气温的极差是( )
| A. | -7°C | B. | 7°C | C. | -9°C | D. | 9°C |
 如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.
如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.
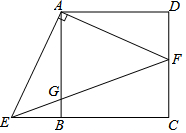 如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.
如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.