Question

20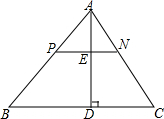．如图，PN∥BC，AD⊥BC交PN于点E，交BC于点D．
（1）若PB：AP=$\sqrt{3}$：1，求$\frac{AE}{AD}$的值．
（3）若BC=15cm，AD=10cm，且PN=ED=x，求x的值．

Answer 1

分析 （1）由已知条件得出AB：AP=（$\sqrt{3}$+1）：1，由平行线分线段成比例定理得出$\frac{AE}{AD}=\frac{AP}{AB}$，即可得出结果；
（2）由平行线得出△APN∽△ABC，得出对应高的比等于相似比$\frac{AE}{AD}$=$\frac{PN}{BC}$，得出方程，解方程即可．

解答 解：（1）∵PB：AP=$\sqrt{3}$：1，
∴AB：AP=（$\sqrt{3}$+1）：1，
∵PN∥BC，
∴$\frac{AE}{AD}=\frac{AP}{AB}$=$\frac{1}{\sqrt{3}+1}$=$\frac{\sqrt{3}-1}{2}$；
（2）∵PN∥BC，
∴△APN∽△ABC，
∴$\frac{AE}{AD}$=$\frac{PN}{BC}$，
即$\frac{10-x}{10}=\frac{x}{15}$，
解得：x=6．

点评 本题考查了平行线分线段成比例定理、比例的性质、相似三角形的判定与性质；熟练掌握平行线分线段成比例定理，由相似三角形的性质得出对应高的比等于相似比是解决（2）的关键．