题目内容
8．
如图，在等腰梯形ABCD中．AD∥BC，过C作CE∥AB．P为梯形ABCD内一点，连结BP并延长交CD于F，交CE于E，再连结PC．若BP=PC．求证：△PFC∽△PCE．
分析 如图，由PB=PC得∠1=∠2，由四边形ABCD为等腰梯形得到∠1+∠3=∠2+∠4，则∠3=∠4，再利用平行线的性质得∠3=∠E，所以∠4=∠E，加上∠FPC=∠CPE，于是根据有两组角对应相等的两个三角形相似即可得到结论．
解答 解：如图，
∵PB=PC，
∴∠1=∠2，
∵四边形ABCD为等腰梯形，
∴∠ABC=∠DCB，
即∠1+∠3=∠2+∠4，
∴∠3=∠4，
∵CE∥AB，
∴∠3=∠E，
∴∠4=∠E，
而∠FPC=∠CPE，
∴△PFC∽△PCE．
点评 本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．也考查了等腰梯形的性质．
练习册系列答案
名校课堂系列答案
相关题目
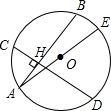如图，在⊙O中，弦AB⊥CD，H为垂足，AE是O的直径．求证：HA2+HD2+HC2+HB2=AE2．
如图所示，化简|a|-|c|+|a-c|-2|c-b|+|b+c|．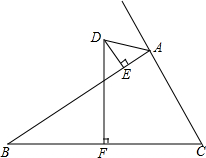
如图，在△ABC中，AB＞AC，BC的垂直平分线DF交△ABC的外角平分线AD于点D，DE⊥AB于点E，线段AC，AE，BE之间有怎样的关系？请写出你的猜想，并加以证明．
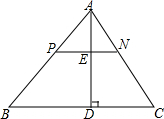如图，PN∥BC，AD⊥BC交PN于点E，交BC于点D．