题目内容
5．
已知，如图，AB为直径，AD=DC=BC，则∠CBA=60度．
分析 根据圆心角、弧、弦的关系得出$\widehat{AD}$=$\widehat{DC}$=$\widehat{BC}$，度数为60°，从而得出$\widehat{AC}$的度数为120°，然后根据圆周角定理即可求得．
解答 解：∵AB为直径，AD=DC=BC，
∴$\widehat{AD}$=$\widehat{DC}$=$\widehat{BC}$，度数为60°，
∴$\widehat{AC}$的度数为120°，
∴∠CBA=60°，
故答案为60．
点评 本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了等边三角形的判定与性质．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
如图所示，已知点P和直线l，求作：点P关于直线l的对称点P′．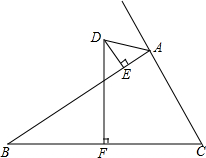
如图，在△ABC中，AB＞AC，BC的垂直平分线DF交△ABC的外角平分线AD于点D，DE⊥AB于点E，线段AC，AE，BE之间有怎样的关系？请写出你的猜想，并加以证明．
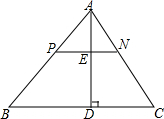如图，PN∥BC，AD⊥BC交PN于点E，交BC于点D．
如图，四边形ABCD中，DA=DB=DC，∠ADC=110°，求∠ABC的度数．