题目内容
13.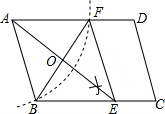 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
分析 (1)由尺规作∠BAF的角平分线的过程可得,AB=AF,∠BAE=∠FAE,根据平行四边形的性质可得∠FAE=∠AEB,然后证明AF=BE,进而可得四边形ABEF为平行四边形,再由AB=AF可得四边形ABEF为菱形;
(2)根据菱形的性质可得AE⊥BF,BO=$\frac{1}{2}$FB=3,AE=2AO,利用勾股定理计算出AO的长,进而可得AE的长.
解答 (1)证明:由尺规作∠BAF的角平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=FA,
∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形;
(2)解:∵四边形ABEF为菱形,
∴AE⊥BF,BO=$\frac{1}{2}$FB=3,AE=2AO,
在Rt△AOB中,AO=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AE=2AO=8.
点评 此题主要考查了菱形的性质和判定,关键是掌握一组邻边相等的平行四边形是菱形,菱形对角线互相垂直且平分.

练习册系列答案
相关题目
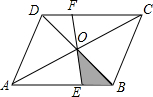 如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.
如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.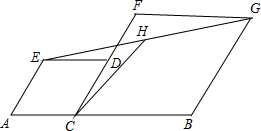 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.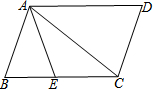 如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1.
如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1.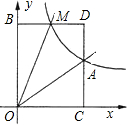 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.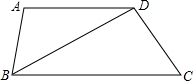 如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.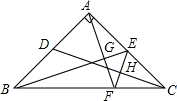 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )