题目内容
4.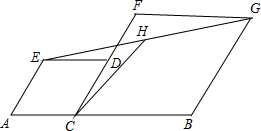 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
分析 连接AD,CE,CG,根据菱形的性质可知AD⊥CE,∠CAD=$\frac{1}{2}$∠EAC,∠BCG=$\frac{1}{2}$∠BCF,根据平行线的性质可得出∠EAC=∠BCF,故可得出∠CAD=∠BCG,所以AD∥CG,即CE⊥CG,再由直角三角形的性质即可得出结论.
解答  解:连接AD,CE,CG,
解:连接AD,CE,CG,
∵四边形ACDE与四边形BCFG均是菱形,
∴AD⊥CE,∠CAD=$\frac{1}{2}$∠EAC,∠BCG=$\frac{1}{2}$∠BCF.
∵AE∥CF,
∴∠EAC=∠BCF,
∴∠CAD=∠BCG,
∴AD∥CG,
∴CE⊥CG.
∵H是EG的中点,EG=4,
∴CH=$\frac{1}{2}$EG=2.
故答案为:2.
点评 本题考查的是菱形的性质,根据题意作出辅助线,构造出直角三角形,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
14.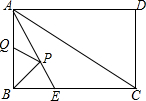 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
19.使不等式x-4>4x-1成立的值中最大的整数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | 2 |
 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.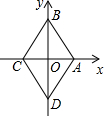 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
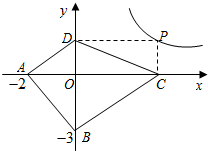
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$). 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.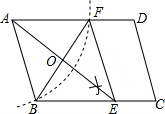 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.