题目内容
3.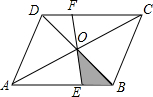 如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.
如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.(1)求证:BE=DF;
(2)如果E、F分别是这条直线与CB,AD的延长线的交点,是否仍然有BE=DF?若有,请证明;
(3)当BE=$\frac{1}{m}$AB时,若△BOE的面积为S,将?ABCD的面积用含m,S的式子表示出来.
分析 (1)根据平行四边形的性质可得DO=BO,DC∥AB,根据平行线的性质可得∠CDO=∠OBE,然后再利用ASA判定△FDO≌△EBO可得DF=EB;
(2)根据平行四边形的性质可得DO=BO,DA∥CB,根据平行线的性质可得∠E=∠F,然后再利用AAS判定△FDO≌△EBO可得DF=EB;
(3)过O作OM⊥AB,根据三角形的面积公式可得S△ABO=mS△BOE=mS,根据平行四边形的面积可得S平行四边形ABCD=4S△AOB,进而可得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴DO=BO,DC∥AB,
∴∠CDO=∠OBE,
在△FDO和△EBO中$\left\{\begin{array}{l}{∠FDO=∠EBO}\\{BO=DO}\\{∠DOF=∠EOB}\end{array}\right.$,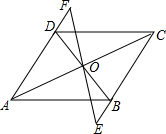
∴△FDO≌△EBO(ASA),
∴DF=EB;
(2)仍然有BE=DF,
证明:∵四边形ABCD是平行四边形,
∴DO=BO,DA∥CB,
∴∠F=∠E,
在△FDO和△EBO中,$\left\{\begin{array}{l}{∠F=∠E}\\{∠FOD=∠EOB}\\{DO=BO}\end{array}\right.$,
∴△FDO≌△EBO(ASA),
∴DF=EB;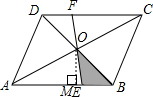
(3)如图:过O作OM⊥AB,
∵S△ABO=$\frac{1}{2}×$OM×AB,S△BOE=$\frac{1}{2}$•OM×EB,BE=$\frac{1}{m}$AB,
∴S△ABO=mS△BOE=mS,
∵四边形ABCD是平行四边形,
∴S平行四边形ABCD=4S△AOB,
∴S平行四边形ABCD=4mS.
点评 此题主要考查了平行四边形的性质,以及平行四边形的面积,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案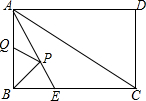 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
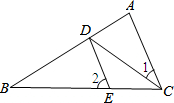 如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.
如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.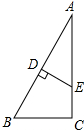 如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.
如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.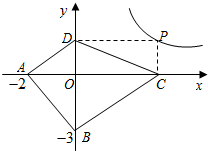 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.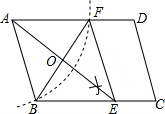 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.