题目内容
2.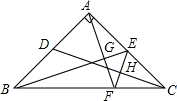 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据已知条件得到∠ABC=45°,根据余角的性质得到∠EAF=∠ABE,由于∠ABE+∠EBF=∠ABC=45°,于是得到∠FAE+∠EBF=45°;故①正确;由∠ABC=∠EAG,∠AGB=∠AGE=90°,推出△ABG∽△AEG,根据相似三角形的性质得到$\frac{AG}{GE}$=$\frac{BG}{AG}$;故②正确;过点C作CM⊥AC交AF延长线于点M,易证△ABE≌△CAM,可得AE=CM,∠AEB=∠M,即可证明△EFC≌△MCF,可得∠FEC=∠M,即可证明△ABE≌△ACD,可得∠ABE=∠ACD,于是得到EF⊥CD,故③正确;根据等腰三角形的性质即可得到故CE≠CF④错误.
解答 解:∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∵AF⊥BE,
∴∠EAF+∠BAF=∠ABG+∠BAF=90°,
∴∠EAF=∠ABE,
∵∠ABE+∠EBF=∠ABC=45°,
∴∠FAE+∠EBF=45°;
故①正确;
∵∠ABC=∠EAG,∠AGB=∠AGE=90°,
∴△ABG∽△AEG,
∴$\frac{AG}{GE}$=$\frac{BG}{AG}$;故②正确;
如图,过点C作CM⊥AC交AF延长线于点M,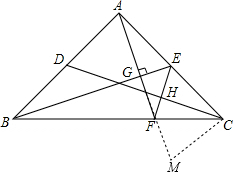
在△ABE和△CAM中,$\left\{\begin{array}{l}{∠ABE=∠EAF}\\{AB=AC}\\{∠BAC=∠ACM}\end{array}\right.$,
∴△ABE≌△CAM(ASA),
∴AE=CM,∠AEB=∠M,
∵AE=EC,
∴EC=CM,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ACM=90°,
∴∠FCM=90-45°=45°=∠ACF,
在△EFC和△MFC中,$\left\{\begin{array}{l}{EC=MC}\\{∠FCM=∠ECF}\\{CF=CF}\end{array}\right.$,
∴△EFC≌△MCF(SAS),
∴∠FEC=∠M,
∴∠FEC=∠FCM,
∵AB=AC,点D、E分别是AB、AC边的中点,
∴AD=AE,
在△ABE与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD,
∴∠ACD+∠FEC=90°,
∴∠EHC=90°,
∴EF⊥CD,故③正确;
∵AD=BD,AC≠BC,
∴∠ACD≠∠BCD,
∵EF⊥CD,
∴CE≠CF;故④错误.
故选C.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△CAM、△EFC≌△MCF和△ABE≌△ACD是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案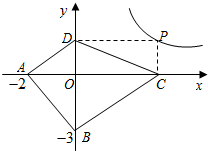 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.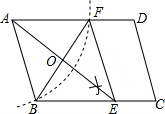 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.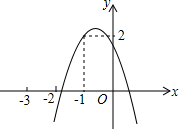 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论:
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论: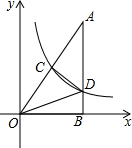 如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.
如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.