题目内容
某校把一块沿河的三角形废地（如图）开辟为生物园，现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分．（1）请你用尺和圆规在图中作出小路CD（不写作法，保留作图痕迹）
（2）若∠CAB=60°，AC=8，求C处到河岸的最短距离．
考点：作图—应用与设计作图,解直角三角形的应用
专题：
分析：（1）作出线段AB的垂直平分线，找到AB中点，进而得出答案；
（2）利用sin∠CAE=
=
求出CE即可．
（2）利用sin∠CAE=
| CE |
| CA |
| ||
| 2 |
解答：
解：（1）即CD是所求作的小路；
（2）如图，过点C作CE垂直AB于点E，
在RT△CAE中，∵CA=8，∠CAE=60°，
∴sin∠CAE=
=
∴CE=
×AC=4
答：C到河岸的最短距离为4
．
解：（1）即CD是所求作的小路；（2）如图，过点C作CE垂直AB于点E，
在RT△CAE中，∵CA=8，∠CAE=60°，
∴sin∠CAE=
| CE |
| CA |
| ||
| 2 |
∴CE=
| ||
| 2 |
| 3 |
答：C到河岸的最短距离为4
| 3 |
点评：此题主要考查了应用设计与作图以及三角形中线的性质，熟练利用锐角三角函数关系得出是解题关键．
练习册系列答案
阶梯计算系列答案
相关题目
已知某条经过原点的直线还经过点（2，1），下列结论正确的是（ ）
| A、直线的解析式为y=2x |
| B、函数图象经过二、四象限 |
| C、函数图象一定经过点（-2，-1） |
| D、y随x的增大而减小 |
某车间有28名工人生产螺丝和螺母，已知平均每人每天可生产螺丝12个或螺母18个，一个螺丝配两个螺母．若安排x名工人生产螺丝，y名工人生产螺母才能使每天生产的正品正好配套，则可得方程组（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
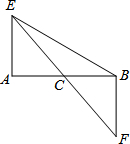如图，C是线段AB的中点，AE⊥AB，BF⊥AB，过点C的直线与AE、BF分别交于点E、F．
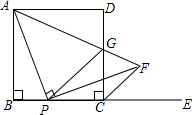如图，在正方形ABCD中，AB=5，P是BC边上任意一点，E是BC延长线上一点，连接AP，作PF⊥AP，使PF=PA，连接CF，AF，AF交CD边于点G，连接PG．