题目内容
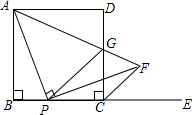 如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形?若存在,求出BM的长度;若不存在,说明理由.
考点:正方形的性质,全等三角形的判定与性质,平行四边形的判定
专题:
分析:(1)过点F作FH⊥BE于点H,利用正方形的性质,证得△BAP≌△HPF得出PH=AB,BP=FH进一步得出BP+PC=PC+CH,CH=BP=FH,∠FHC=90°,求得∠DCF=90°-45°=45°得出结论;
(2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;
(3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可.
(2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;
(3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可.
解答:(1)证明:如图,

过点F作FH⊥BE于点H,
∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90°,AB=BC,
∴∠BAP+∠APB=90°
∵AP⊥PF,
∴∠APB+∠FPH=90°
∴∠FPH=∠BAP
在△BAP和△HPF中,∠ABP=∠PHF
在△BAP和△HPF中,
,
∴△BAP≌△HPF(AAS)
∴PH=AB,BP=FH
∴PH=BC
∴BP+PC=PC+CH
∴CH=BP=FH …
而∠FHC=90°.
∴∠FCH=CFH=45°
∴∠DCF=90°-45°=45°
∴∠GCF=∠FCE;
(2)PG=PB+DG
证明:如图,

延长PB至K,使BK=DG,连接AK,
∵四边形ABCD是正方形
∴AB=AD,∠ABK=ADG=90°
在△ABK和△ADG中,
,
∴△ABK≌△ADG(SAS)
∴AK=AG,∠KAB=∠GAD,
而∠APF=90°,AP=PF
∴∠PAF=∠PFA=45°
∴∠BAP+∠KAB=∠KAP=45°=∠PAF
在△KAP和△GAP中,
,
∴△KAP≌△GAP(SAS)
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG;
(3)存在.
如图,

在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠DAM=90°
在Rt△ABP和Rt△DAM中
∴Rt△ABP≌Rt△DAM(HL)
∴AM=BP=2,
∴BM=AB-AM=5-2=3.
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.

过点F作FH⊥BE于点H,
∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90°,AB=BC,
∴∠BAP+∠APB=90°
∵AP⊥PF,
∴∠APB+∠FPH=90°
∴∠FPH=∠BAP
在△BAP和△HPF中,∠ABP=∠PHF
在△BAP和△HPF中,
|
∴△BAP≌△HPF(AAS)
∴PH=AB,BP=FH
∴PH=BC
∴BP+PC=PC+CH
∴CH=BP=FH …
而∠FHC=90°.
∴∠FCH=CFH=45°
∴∠DCF=90°-45°=45°
∴∠GCF=∠FCE;
(2)PG=PB+DG
证明:如图,

延长PB至K,使BK=DG,连接AK,
∵四边形ABCD是正方形
∴AB=AD,∠ABK=ADG=90°
在△ABK和△ADG中,
|
∴△ABK≌△ADG(SAS)
∴AK=AG,∠KAB=∠GAD,
而∠APF=90°,AP=PF
∴∠PAF=∠PFA=45°
∴∠BAP+∠KAB=∠KAP=45°=∠PAF
在△KAP和△GAP中,
|
∴△KAP≌△GAP(SAS)
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG;
(3)存在.
如图,

在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠DAM=90°
在Rt△ABP和Rt△DAM中
|
∴Rt△ABP≌Rt△DAM(HL)
∴AM=BP=2,
∴BM=AB-AM=5-2=3.
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.
点评:此题考查了正方形的性质,结合了三角形全等的判定与性质,属于综合性比较强的题目,并涉及到探究性试题,解决本类试题要先求解,然后给出结论,再进行证明.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
在Rt△ABC中,∠ACB=90°,∠A=30°,AC=
cm,则AB边上的中线长为( )
| 3 |
| A、1cm | ||
| B、1.5cm | ||
| C、2cm | ||
D、
|
我市某楼盘原准备以每平方米8800元的价格对外销售,但是受国家楼市调控政策的影响,对价格进行了两次下调,最终的销售价格是每平方米6860元.设平均每次下调的百分率是x,可得方程( )
| A、6860(1+x)+6860(1+x)x=8800 |
| B、6860(1+x)2=8800 |
| C、8800(1-x)x=6860 |
| D、8800(1-x)2=6860 |
 某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分.
某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分. 已知平行四边形ABCD,AB=3,AD=5.
已知平行四边形ABCD,AB=3,AD=5.