题目内容
已知某条经过原点的直线还经过点(2,1),下列结论正确的是( )
| A、直线的解析式为y=2x |
| B、函数图象经过二、四象限 |
| C、函数图象一定经过点(-2,-1) |
| D、y随x的增大而减小 |
考点:待定系数法求正比例函数解析式,正比例函数的性质
专题:
分析:首先利用待定系数法求得直线方程,然后根据图象直接作出判断.
解答: 解:设该直线为y=kx(k≠0),则
解:设该直线为y=kx(k≠0),则
1=2k,
解得 k=
.
则该直线方程是:y=
x.
故A错误;
图象如图所示:直线经过第一、三象限,故B错误;
根据正比例函数的中心对称性,知函数图象一定经过点(-2,-1).故C正确;
图象是y随x值的增大而增大,故D错误;
故选:C.
 解:设该直线为y=kx(k≠0),则
解:设该直线为y=kx(k≠0),则1=2k,
解得 k=
| 1 |
| 2 |
则该直线方程是:y=
| 1 |
| 2 |
故A错误;
图象如图所示:直线经过第一、三象限,故B错误;
根据正比例函数的中心对称性,知函数图象一定经过点(-2,-1).故C正确;
图象是y随x值的增大而增大,故D错误;
故选:C.
点评:本题考查了待定系数法求正比例函数解析式,正比例函数的性质.解题时,利用了“数形结合”的数学思想,使问题变得形象化、直观化.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知
(a-
)<0,则a的取值范围是( )
| a |
| 3 |
| A、a≥0 | ||
B、a<
| ||
| C、a>0 | ||
D、0<a<
|
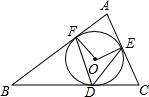 如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )
如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )| A、45° | B、55° |
| C、50° | D、70° |
在Rt△ABC中,∠ACB=90°,∠A=30°,AC=
cm,则AB边上的中线长为( )
| 3 |
| A、1cm | ||
| B、1.5cm | ||
| C、2cm | ||
D、
|
 如图,点E在AD的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能判定AB∥CD的是( )①∠1=∠4;②∠2=∠3;③∠A=∠CDE;④∠C=∠CDE;⑤∠A+∠ADC=180°.
| A、①③ | B、①③⑤ |
| C、②③⑤ | D、②④⑤ |
要使?ABCD成为矩形,下列添加条件正确的是( )
| A、AB=BC |
| B、AC⊥BD |
| C、AC=BD |
| D、∠ABC=∠CDA |
 如图,直线AB∥CD,∠B=100°,∠F=70°,则∠E等于( )度.
如图,直线AB∥CD,∠B=100°,∠F=70°,则∠E等于( )度.| A、30 | B、40 | C、50 | D、60 |
 某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分.
某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分.