题目内容
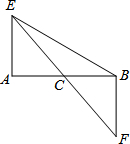 如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.
如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.(1)求证:CE=CF;
(2)若∠F=45°,BF=2,求BE的长.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)根据ASA,可证明△ACE≌BCF,根据全等三角形的性质,可得证明的结论;
(2)根据全等三角形的性质,可得AE的长,根据等腰直角三角形的性质,可得BC的长,根据勾股定理,可得答案.
(2)根据全等三角形的性质,可得AE的长,根据等腰直角三角形的性质,可得BC的长,根据勾股定理,可得答案.
解答:(1)证明:∵C是线段AB的中点,
∴AC=BC
AE⊥AB,BF⊥AB,
∴∠EAC=∠FBC=90°
又∠ACE=∠BCF
∴△ACE≌△BCF
∴CE=CF
(2)解:∵△ACE≌△BCF
∴AE=BF=2.
在△BCF中,∠F=45°,∠FBC=90°
∠BCF=90°-45°=45°
∴BC=BF=2
∴AB=2BF=4
在Rt△ABE中,由勾股定理得
BE=
=
=2
.
∴AC=BC
AE⊥AB,BF⊥AB,
∴∠EAC=∠FBC=90°
又∠ACE=∠BCF
∴△ACE≌△BCF
∴CE=CF
(2)解:∵△ACE≌△BCF
∴AE=BF=2.
在△BCF中,∠F=45°,∠FBC=90°
∠BCF=90°-45°=45°
∴BC=BF=2
∴AB=2BF=4
在Rt△ABE中,由勾股定理得
BE=
| AE2+AB2 |
| 22+42 |
| 5 |
点评:本题考查了全等三角形的性质与判定,(1)利用ASA证明三角形全等,再利用性质证明对应边相等;(2)利用勾股定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
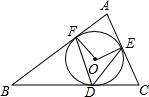 如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )
如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )| A、45° | B、55° |
| C、50° | D、70° |
 如图,直线AB∥CD,∠B=100°,∠F=70°,则∠E等于( )度.
如图,直线AB∥CD,∠B=100°,∠F=70°,则∠E等于( )度.| A、30 | B、40 | C、50 | D、60 |
二元一次方程组
的解为( )
|
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|

 某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分.
某校把一块沿河的三角形废地(如图)开辟为生物园,现学校准备从点C处向河岸AB修一条小路CD将生物园分割成面积相等的两部分.