题目内容
4.已知△ABC中,AB=AC=5,BC=8,点D在BC边上移动,连接AD,将△ADC沿直线AD翻折,点C的对应点为C1.(1)当AC1⊥BC时,CD的长是多少?
(2)如果CD=3,请求出△AC1D与△ABC重叠部分的面积;
(3)当CD≤4时,在点D移动的过程中,是否存在△BC1D为直角三角形的情形?若存在,求出CD的长;若不存在,请说明理由.
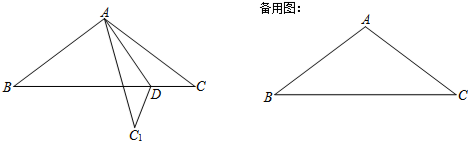
分析 (1)当AC1与BC垂直时,点E是BC的中点,有CE=$\frac{1}{2}$BC=4,由勾股定理可求得AE=3,由于C1D=CD,A1C=AC,在Rt△C1DE中,由勾股定理可求得ED的值,再求得CD的值;
(2)易证△ABE∽△D1CE,得到AB:C1D=AE:ED=BE:EC1,先求得ED,再得到BE与CD的关系式;
(3)分两种情况:当C1E=ED时和当C1E=C1D时,可由(2)中的关系式求得.
解答 解:(1)如下图,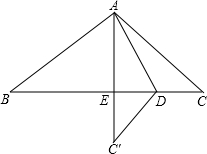
设AC1交边BC于点E.
∵AC1与BC垂直,AB=AC=5,BC=8,
∴CE=$\frac{1}{2}$BC=4,
在Rt△AEC中,AE=$\sqrt{{AC}^{2}{-CE}^{2}}$=3,
∵C1D=CD,AC1=AC=5,EC1=AC1-AE,ED=EC-CD,
∴在Rt△EDC1中,有ED2+EC12=C1D2,即CD2=(5-3)2+(4-CD)2,
解得:CD=$\frac{5}{2}$;
(2)
∵AB=AC,
∴∠B=∠C,
∵∠C1=∠C,
∴∠C1=∠B,
又∵∠AEB=∠DEC1,
∴△AEB∽△DEC1,
∴AB:DC1=AE:DE=BE:C1E,
∴5:C1D=AE:(8-BE-CD)=BE:(5-AE),
∵BE=y,CD=C1D=x,
∴5:x=AE:(8-y-x)=y:(5-AE),
解得AE=$\frac{25-xy}{5}$,y=$\frac{50(x-4)}{{x}^{2}-25}$(0<x<4);
(3)存在.
当C1E=ED时,由于△AEB∽△DEC1,
则有y=BE=AE=$\frac{25-xy}{5}$,
∴y=$\frac{25}{x+5}$,
∴$\frac{25}{x+5}=\frac{50(x-4)}{{x}^{2}-25}$,
∴x=3,
∴CD=3,
当C1E=C1D时,由于△AEB∽△DEC1,则有y=$\frac{50(x-4)}{{x}^{2}-25}$=BE=AB=5,
∴x=5-$\sqrt{10}$或x=5+$\sqrt{10}$(舍),
∴CD=5-$\sqrt{10}$,
存在△BC1D为直角三角形,此时CD=3,或CD=5-$\sqrt{10}$.
点评 此题是几何变换综合题,主要考查了翻折的性质、勾股定理、相似三角形的判定和性质、等腰三角形的性质.用相似建立相等关系是解本题的关键.

 阅读快车系列答案
阅读快车系列答案①将图形A平移后得到图形,则它们是位似图形;
②将图形A绕某点旋转180°后得到图形B,则它们是位似图形;
③两个关于某直线成轴对称的图形一定是位似图形;
④关于某点成中心对称的两个图形一定是位似图形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 B.
B.  C.
C.  D.
D. 
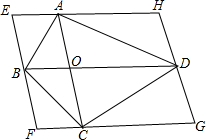 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.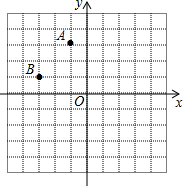 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)