题目内容
1.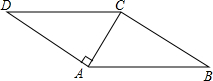 如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8.
如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8.
分析 由平行四边形的性质得出AD=BC,AB=CD,∠D=∠B=30°,由含30°角的直角三角形的性质得出CD=2AC=4,由勾股定理求出AD,即可得出?ABCD的周长.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠D=∠B=30°,
∵AC⊥AD,
∴∠DAC=90°,
∴CD=2AC=4,
∴AD=$\sqrt{C{D}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∴ABCD的周长=2(AD+CD)=2(2$\sqrt{3}$+4)=4$\sqrt{3}$+8;
故答案为:4$\sqrt{3}$+8.
点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出AD是解决问题的关键.

练习册系列答案
相关题目
9.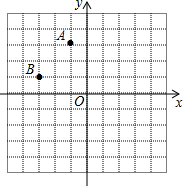 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)
(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
10. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
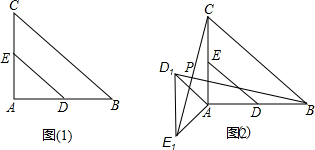 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
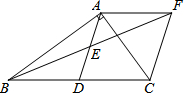 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.