题目内容
2．
如图为实数a，b在数轴上的位置，则（$\sqrt{b}$）2+$\sqrt{（-a）^{2}}$-$\sqrt{（a-b）^{2}}$=0．
分析 根据数轴先确定a、b即a-b的正负，然后根据二次根式性质去根号、合并同类项即可解决问题．
解答 解：根据实数a、b在数轴上的位置得知：
-1＜a＜0＜b＜1，
∴a-b＜0，
则原式=b-a-（b-a）=b-a-b+a=0，
故答案为：0．
点评 本题考查数轴及二次根式的化简，关键是根据数轴得出a、b及a-b的正负情况．
练习册系列答案
相关题目
10．
如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为（ ）
如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为（ ）| A． | 20cm | B． | 22cm | C． | 24cm | D． | 26cm |
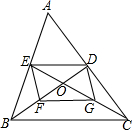如图，△ABC的中线BD、CE相交于点O，F、G分别是OB、OC的中点．
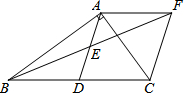在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A做AF∥BC交BE的延长线于点F．