题目内容
7.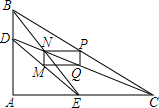 已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
分析 由三角形中位线定理得出MN∥AB,MN=$\frac{1}{2}$BD,PN∥CE,PN=$\frac{1}{2}$CE,MQ∥CE,MQ=$\frac{1}{2}$CE,因此PN=MQ,PN∥MQ,资产四边形PQMN是平行四边形,再由已知条件得出MN⊥MQ,证出∠NMQ=90°,即可得出四边形PQMN是矩形.
解答 证明:∵M,N分别是DE,BE的中点,
∴MN是△BDE的中位线,
∴MN∥AB,MN=$\frac{1}{2}$BD,
同理:PN∥CE,PN=$\frac{1}{2}$CE,MQ∥CE,MQ=$\frac{1}{2}$CE,
∴PN=MQ,PN∥MQ,
∴四边形PQMN是平行四边形,
∵∠A=90°,
∴BA⊥CA,
∵MN∥AB,MQ∥AC,
∴MN⊥MQ,
∴∠NMQ=90°,
∴四边形PQMN是矩形.
点评 本题考查了矩形的判定、平行四边形的判定、三角形中位线定理;熟记矩形的判定,由三角形中位线定理证出PN=MQ,PN∥MQ,MN⊥MQ是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
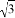 ,AC,BD相交于点O.
,AC,BD相交于点O.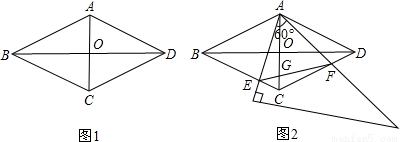
 已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.
已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.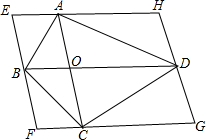 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.