题目内容
20.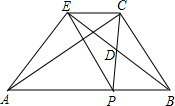 如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.
如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.(1)求证:四边形PBCE是平行四边形;
(2)当四边形PCEA不是梯形时,AP=BP(填“<”、“=”、“>”中的一个);此时四边形PCEA是菱形(填“平行四边形”、“菱形”、“正方形”中的一个),并说明理由.
分析 (1)根据对角线互相平分的四边形是平行四边形即可证明.
(2)先证明四边形APCE是平行四边形,再证明PA=PC即可解决问题.
解答 (1)证明:∵D是PC的中点, ∴CD=DP,
∴CD=DP,
又∵DB=DE,
∴四边形PBCE是平行四边形.
(2)∵四边形PCEA不是梯形时,CE∥AP,
∴AE∥PC,
∴四边形AECP是平行四边形,
∴AP=EC,
∵四边形PBCE是平行四边形,
∴EC=PB,
∴AP=BP,
∵∠ACB=90°,
∴PC=PA=PB,
∵四边形PBCE是平行四边形,又PA=PC,
∴四边形APCE是菱形.
故答案分别为=,菱形.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、直角三角形斜边中线定理等知识,熟练掌握平行四边形、菱形的判定方法是解题的关键,属于中考常考题型.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
15.下列说法正确的有( )
①将图形A平移后得到图形,则它们是位似图形;
②将图形A绕某点旋转180°后得到图形B,则它们是位似图形;
③两个关于某直线成轴对称的图形一定是位似图形;
④关于某点成中心对称的两个图形一定是位似图形.
①将图形A平移后得到图形,则它们是位似图形;
②将图形A绕某点旋转180°后得到图形B,则它们是位似图形;
③两个关于某直线成轴对称的图形一定是位似图形;
④关于某点成中心对称的两个图形一定是位似图形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.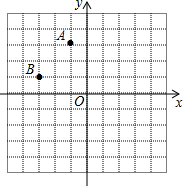 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)
(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
10. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
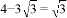 B.
B. 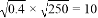 C.
C. 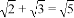 D.
D. 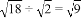
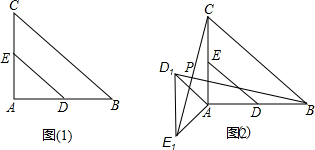 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.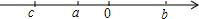 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.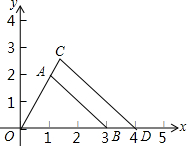 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.