题目内容
1.市体校射击队要从甲、乙两名射击队员中挑选一人参加省级比赛,因此,让他们在相同条件下各射击10次,成绩如图所示.为分析成绩,教练根据统计图算出了甲队员成绩的平均数为8.5环、方差为1.05,请观察统计图,解答下列问题:
(1)先写出乙队员10次射击的成绩,再求10次射击成绩的平均数和方差;
(2)根据两人成绩分析的结果,若要选出总成绩高且发挥稳定的队员参加省级比赛,你认为选出的应是甲,理由是:平均数高,且成绩稳定.

分析 (1)根据平均数的公式:平均数=所有数之和再除以数的个数;方差就是各变量值与其均值离差平方的平均数,根据方差公式计算即可;
(2)根据甲和乙的平均数和方差,选择平均数和方差较小的同学即可.
解答 解;(1)乙队员10次射击的成绩分别为6,7,7,8,8,8,9,9,10,10;
乙10次射击成绩的平均数=(6+2×7+3×8+2×9+2×10)÷10=8.2,
方差=$\frac{1}{10}$[(6-8.2)2+2×(7-8.2)2+3×(8-8.2)3+2×(9-8.2)2+2×(10-8.2)2]=2.2;
(2)∵8.5>8.2,S2甲>S2乙,
∴甲的平均数高,且成绩稳定,
∴选择甲同学参加射击比赛;
故答案为:甲;平均数高,且成绩稳定.
点评 本题考查平均数、方差的定义和公式;熟练掌握平均数和方差的计算是解决问题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
11.如果(x+m)(x+$\frac{1}{4}$)的积不含x的一次项,则m为( )
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | 4 | D. | -4 |
12.若ab<0,则y=ax+b的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
16.已知ax=ay,下列等式成立的是( )
| A. | x=y | B. | 3-ax=3-ay | C. | ax=-ay | D. | x+1=ay-1 |
13. 如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
 如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )| A. | 4m | B. | 7m | C. | 2m | D. | 8m |
16.a、b、c是三角形的三条边长,则代数式a2-c2-2ab+b2的值( )
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 与零的大小无关 |
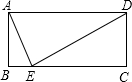 如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.
如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.