题目内容
9.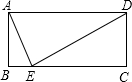 如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.
如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.
分析 由矩形的性质和等腰三角形的性质求出∠ADE=30°,得出∠CED=30°,再由含30°角的直角三角形的性质得出CD=$\frac{1}{2}$DE=7即可.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠C=∠B=∠ADC=90°,AD∥BC,
∴∠CED=∠ADE,
∵∠BAE=15°,
∴∠DAE=90°-15°=75°,
∵AD=DE=14,
∴∠DEA=∠DAE=75°,
∴∠ADE=180°-2×75°=30°,
∴∠CED=30°,
∴CD=$\frac{1}{2}$DE=7;
故答案为:7.
点评 本题考查了矩形的性质、含30°角的直角三角形的性质、等腰三角形的性质、三角形内角和定理等知识;熟练掌握矩形的性质和等腰三角形的性质,求出∠CED=30°是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19. 如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的( )
如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的( )
 如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的( )
如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的( )| A. | 主视图改变,左视图改变 | B. | 俯视图不变,左视图不变 | ||
| C. | 俯视图改变,左视图改变 | D. | 主视图改变,左视图不变 |
17.六边形的对角线共有( )
| A. | 6条 | B. | 8条 | C. | 9条 | D. | 18条 |
4.如果m是任意实数,那么P(m-4,m+4)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14. 如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )
如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )
 如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )
如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )| A. | 75° | B. | 100° | C. | 115° | D. | 120° |
 有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据$\frac{15}{4}$,3,$\frac{16}{5}$,2,$\frac{5}{3}$中可以作为线段AQ长的有3个.
有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据$\frac{15}{4}$,3,$\frac{16}{5}$,2,$\frac{5}{3}$中可以作为线段AQ长的有3个.
 如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的? 如图,∠BAC=120°,AD平分∠BAC,且AD=4,点P是射线AB上一动点,连接DP,△PAD的外接圆于AC交于点Q,则线段QP的最小值是2$\sqrt{3}$.
如图,∠BAC=120°,AD平分∠BAC,且AD=4,点P是射线AB上一动点,连接DP,△PAD的外接圆于AC交于点Q,则线段QP的最小值是2$\sqrt{3}$.